Android自定义控件（一）贝瑟尔曲线
1 前言
贝瑟尔曲线是Android工程师必须要掌握的技能之一。
什么是贝瑟尔曲线，请自行百度、google。
2 原理
1.在平面内选3个不同线的点并且依次用线段连接起来，如下图：
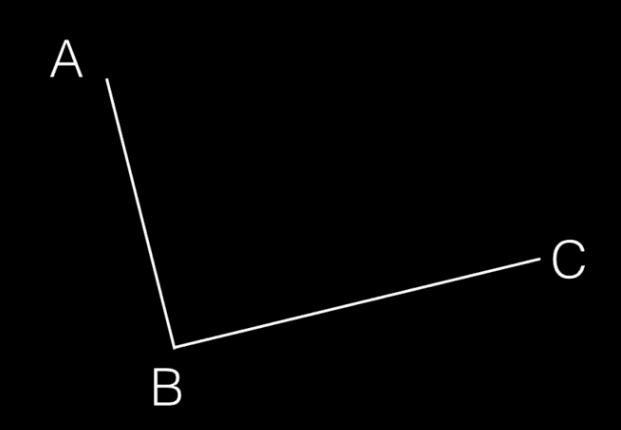
2.在AB和BC线段中找出点D和点E，使得AD/AB = BE/BC，如下图：
3.连接DE，在DE上寻找点F，F点需要满足：DF/DE = AD/AB = BE/BC，如下图：
4.根据DE线段和计算公式找出所有F点，然后将其连接起来，构成曲线。连接规则：已上图为例，第一个连接点就是A-F，第二个连接点就是A-F1（这个F1必须满足DF1/DE = AD/AB = BE/BC）以此类推，直到最后连接上C点
5. 二阶贝瑟尔曲线计算公式：
可以看出P1-P0为曲线在P0处的切线。
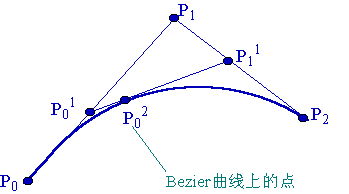6. 计算公式详解：
设P0、P02、P2是一条抛物线上顺序三个不同的点。过P0和P2点的两切线交于P1点，在P02点的切线交P0P1和P2P1于P01和P11，则如下比例成立
当P0，P2固定，引入参数t，令上述比值为t:(1-t)，即有：
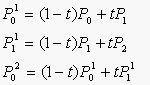
t从0变到1，第一、二式就分别表示控制二边形的第一、二条边，它们是两条一次Bezier曲线。将一、二式代入第三式得：
当t从0变到1时，它表示了由三顶点P0、P1、P2三点定义的一条二次Bezier曲线。
总结：关于贝赛尔曲线的基本数学理论大概就是上面的内容。两个线段根据等比关系找点的贝塞尔曲线，一般也称为二阶贝塞尔曲线。
3 贝瑟尔曲线N阶扩展
N阶贝瑟尔曲线的规则和二阶贝瑟尔曲线的规则都是一样的，都是线段找点，这个点必须满足等比关系，然后点成线。
下面三阶贝瑟尔曲线讲解：
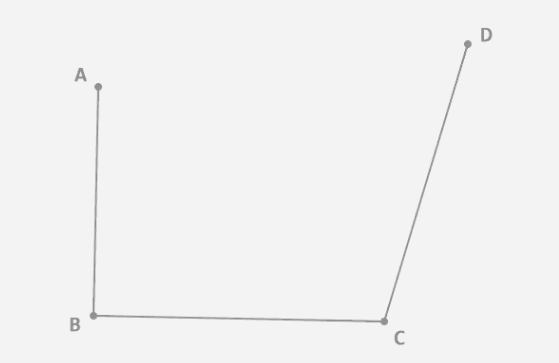
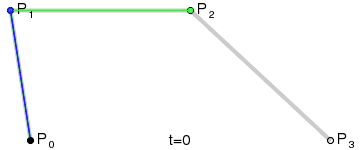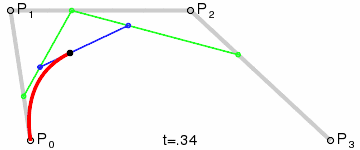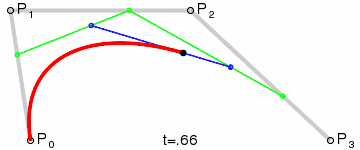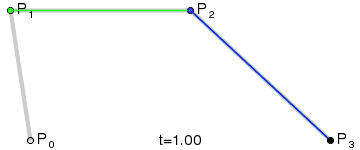
1.三阶贝瑟尔曲线四个点依次用线段连接，如下图：
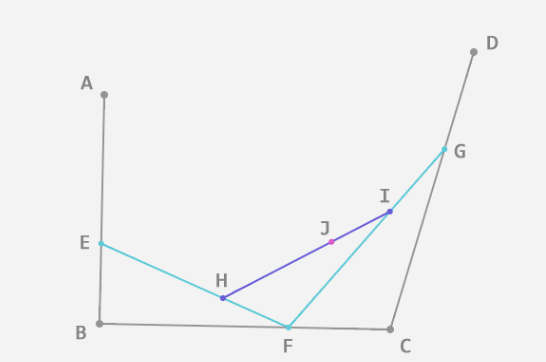
2.找出三条线段上的E、F、G，三点必须满足等比计算规则，同二阶贝瑟尔曲线一样，计算规则：AE/AB = BF/BC = CG/CD。连接EF、FG，接着在EF和FG线段上找到H、I两点，两点依旧需要满足等比计算规则，计算规则：EH/EF = FI/FG。最后连接HI线段，再从HI线段中找到J点，J点也需要满足等比计算规则，计算规则：EH/EF = FI/FG = HJ/HI。如下图所示：
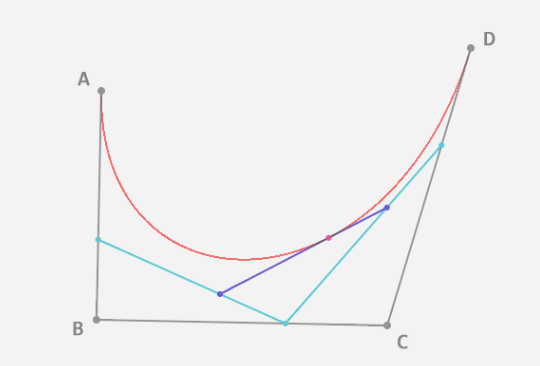
3.重复2的操作，找到所有的J点，依次连接构成曲线，即三阶贝塞尔曲线。如下图：
动图：
4.计算公式：
同理，四阶贝瑟尔曲线实现步骤也是这样的，下面是四阶贝瑟尔曲线实现的动图：
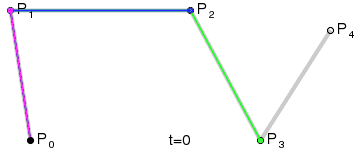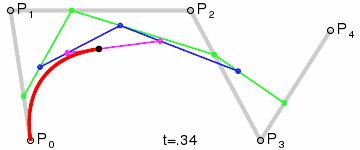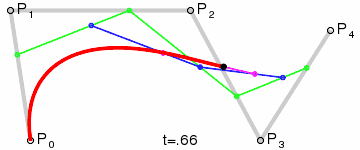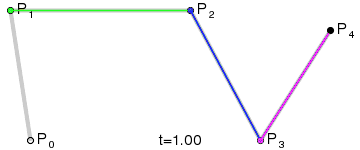
5.五阶....不讲了...看看动图吧。
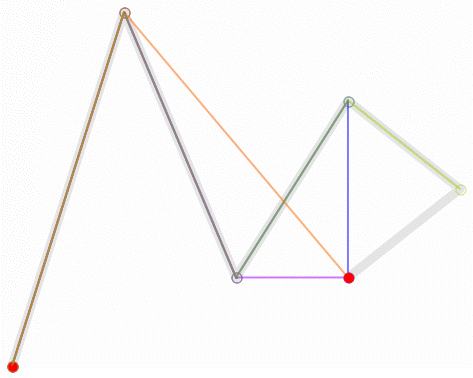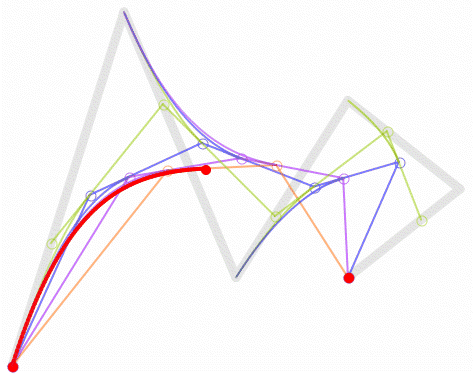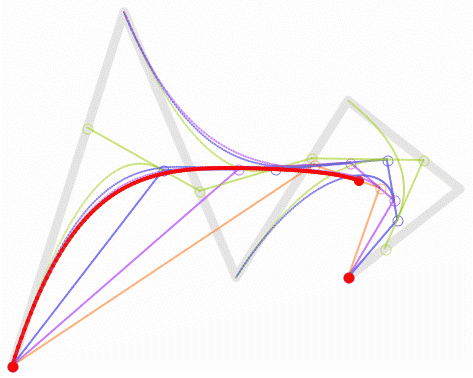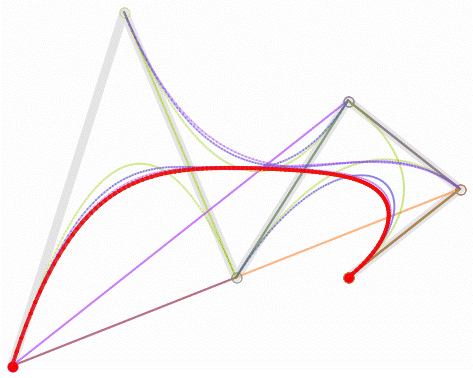
6.一阶贝瑟尔曲线...实现原理没啥好讲的，看一下动图就能理解了。
一阶贝瑟尔曲线计算公式：
可以看出，贝瑟尔曲线不只是可以画曲线，也可以画直线，自定义控件画直线的方法之一（用的不多）。Android属性动画中，系统给我们提供了PathInterpolator插值器，这里面就有贝瑟尔曲线的身影。
7.N阶贝瑟尔曲线通用公式：
8.上面这些可能还不够牛不，那么看看下面：
这里就不做讲解了...想要了解的可以自行google。
9.C/C++实现可以参考：图形算法：贝塞尔曲线
4 贝瑟尔曲线实现的自定义控件
1. 仿沙漏的自定义view
后续补充....
5 参考
2. 贝塞尔曲线 总结
