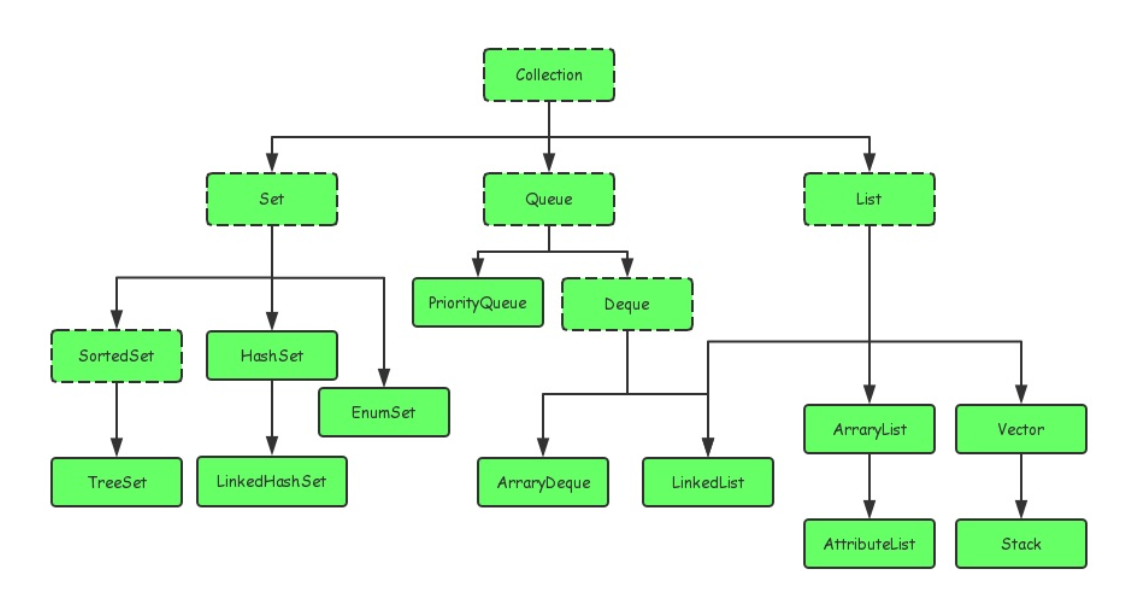
1 简介Java集合大致可以分为Set、List、Queue和Map四种体系。其中Set代表无序、不可重复的集合；List代表有序、重复的集合；而Map则代表具有映射关系的集合。Java 5 又增加了Queue体系集合，代表一种队列集合实现。Java集合就像一种容器，可以把多个对象（实际上是对象的引用，但习惯上都称对象）“丢进”该容器中。从Java 5 增加了泛型以后，Java集合可以记住容器中对象的数据类型，使得编码更加简洁、健壮。1.1 集合和数组的区别①.数组长度在初始化时指定，意味着只能保存定长的数据。而集合可以保存数量不确定的数据。同时可以保存具有映射关系的数据（即关联数组，键值对 key-value）。②.数组元素即可以是基本类型的值，也可以是对象。集合里只能保存对象（实际上只是保存对象的引用变量），基本数据类型的变量要转换成对应的包装类才能放入集合类中。1.2 Java集合类之间的继承关系Java的集合类主要由两个接口派生而出：Collection和Map,Collection和Map是Java集合框架的根接口。面试会经常问到：自己实现 LinkedList、两个栈实现一个队列，数组实现栈，队列实现栈等。1.2.1 Collection其中ArrayList、HashSet、LinkedList、TreeSet是我们经常会有用到的已实现的集合类。1.2.2 Map其中HashMap，TreeMap是我们经常会用到的集合类。2 Collection接口详解2.1 接口方法下面是JDK官方文档给出的定义方法注意：当使用Iterator对集合元素进行迭代时，把集合元素的值传给了迭代变量（就如同参数传递是值传递，基本数据类型传递的是值，引用类型传递的仅仅是对象的引用变量。2.2 Set集合Set集合和Collection基本差不多，Set多了一个不允许重复元素，如果使用add()方法添加重复元素，会添加失败，并且返回false。2.3 List集合2.3.1 概述List集合代表一个元素有序、可重复的集合，集合中每个元素都有其对应的顺序索引。List集合允许使用重复元素，可以通过索引来访问指定位置的集合元素。List集合默认按元素的添加顺序设置元素的索引，例如第一个添加的元素索引为0，第二个添加的元素索引为1......List作为Collection接口的子接口，可以使用Collection接口里的全部方法。而且由于List是有序集合，因此List集合里增加了一些根据索引来操作集合元素的方法。2.3.2 接口方法1. void add(int index, Object element):在列表的指定位置插入指定元素（可选操作）。2. boolean addAll(int index, Collection<? extends E> c) :将集合c 中的所有元素都插入到列表中的指定位置index处。3. Object get(index):返回列表中指定位置的元素。4. int indexOf(Object o):返回此列表中第一次出现的指定元素的索引；如果此列表不包含该元素，则返回 -1。5. int lastIndexOf(Object o):返回此列表中最后出现的指定元素的索引；如果列表不包含此元素，则返回 -1。6. Object remove(int index):移除列表中指定位置的元素。7. Object set(int index, Object element):用指定元素替换列表中指定位置的元素。8. List subList(int fromIndex, int toIndex):返回列表中指定的 fromIndex（包括）和 toIndex（不包括）之间的所有集合元素组成的子集。9. Object[] toArray():返回按适当顺序包含列表中的所有元素的数组（从第一个元素到最后一个元素）。2.3.3 ArrayList集合2.3.3.1 概述java.util.ArrayList集合数据存储的结构是数组结构。节约空间，但数组有容量限制。超出限制时会增加50%容量，用System.arraycopy()复制到新的数组，因此最好能给出数组大小的预估值。默认第一次插入元素时创建大小为10的数组。按数组下标访问元素—get(i)/set(i,e) 的性能很高，这是数组的基本优势。直接在数组末尾加入元素—add(e)的性能也高，但如果按下标插入、删除元素—add(i,e), remove(i), remove(e)，则要用System.arraycopy()来移动部分受影响的元素，性能就变差了，这是基本劣势。更加详细的源码解刨可以查看 参考 从源码角度认识ArrayList，LinkedList与HashMap2.3.3.2 特点1. 遍历和随机访问的速度快2. 增删对象的效率就低，因为底层的实现是通过数组来实现3. 数组结构2.3.3.3 add()函数当我们在ArrayList中增加元素的时候，会使用add函数。他会将元素放到末尾。具体实现如下：publicbooleanadd(E e){ ensureCapacityInternal(size + 1); // Increments modCount!! elementData[size++] = e; return true; }ensureCapacityInternal()这个函数就是扩容机制的核心。下面是这个函数的实现private void ensureCapacityInternal(int minCapacity) { if (elementData == DEFAULTCAPACITY_EMPTY_ELEMENTDATA) { minCapacity = Math.max(DEFAULT_CAPACITY, minCapacity); } ensureExplicitCapacity(minCapacity); } private void ensureExplicitCapacity(int minCapacity) { modCount++; // overflow-conscious code if (minCapacity - elementData.length > 0) grow(minCapacity); } private void grow(int minCapacity) { // overflow-conscious code int oldCapacity = elementData.length; // 扩为1.5倍 int newCapacity = oldCapacity + (oldCapacity >> 1); // 1.5倍不满足需求，直接扩为需求值 if (newCapacity - minCapacity < 0) newCapacity = minCapacity; if (newCapacity - MAX_ARRAY_SIZE > 0) newCapacity = hugeCapacity(minCapacity); // minCapacity is usually close to size, so this is a win: elementData = Arrays.copyOf(elementData, newCapacity); } private static int hugeCapacity(int minCapacity) { if (minCapacity < 0) // overflow throw new OutOfMemoryError(); return (minCapacity > MAX_ARRAY_SIZE) ? Integer.MAX_VALUE : MAX_ARRAY_SIZE; }可以看出，在ArrayList中，当它的大小不满足需求时，那么就将数组变为原长度的1.5倍，之后把旧数据移到新的数组里。2.3.3.4 set()和get()函数首先看看源码：public E get(int index) { if (index >= size) throw new IndexOutOfBoundsException(outOfBoundsMsg(index)); return (E) elementData[index]; } public E set(int index, E element) { if (index >= size) throw new IndexOutOfBoundsException(outOfBoundsMsg(index)); E oldValue = (E) elementData[index]; elementData[index] = element; return oldValue; }set和get方法都是首先对index进行检查，然后再进行赋值或者访问操作。2.3.3.5 remove()函数首先还是先看源码：public E remove(int index) { if (index >= size) throw new IndexOutOfBoundsException(outOfBoundsMsg(index)); modCount++; E oldValue = (E) elementData[index]; int numMoved = size - index - 1; if (numMoved > 0) // 把后面的往前移 System.arraycopy(elementData, index+1, elementData, index, numMoved); // 把最后的置null elementData[--size] = null; // clear to let GC do its work return oldValue; }看源码应该都能看懂，也是先对index进行检查，最重要是System.arraycopy，把数组往前移了一位，然后把最后一位置null。2.3.4 LinkedList2.3.4.1 概述以双向链表实现。链表无容量限制，但双向链表本身使用了更多空间，也需要额外的链表指针操作。按下标访问元素—get(i)/set(i,e) 要悲剧的遍历链表将指针移动到位(如果i>数组大小的一半，会从末尾移起)。插入、删除元素时修改前后节点的指针即可，但还是要遍历部分链表的指针才能移动到下标所指的位置，只有在链表两头的操作—add()，addFirst()，removeLast()或用iterator()上的remove()能省掉指针的移动。LinkedList是一个简单的数据结构，与ArrayList不同的是，它是基于链表实现的。更加详细的源码解刨可以查看 参考 从源码角度认识ArrayList，LinkedList与HashMap2.3.4.2 特点1. 链结构2. 方便元素添加，删除的集合3. 访问元素的效率不高使用LinkedList集合特有的方法，不能使用多态public void addFirst(E e):将指定元素插入此列表的开头public void addLast(E e):将指定元素添加到此列表的结尾public void addpush(E e):将元素推如此列表所表示的推栈 public E getFirst():返回此列表的第一个元素。public E getLast():返回此列表的最后一个元素。 public E removeFirst():移除并返回此列表的第一个元素。public E removeLast():移除并返回此列表的最后一个元素。public E pop():从此列表所表示的推栈处弹出一个元素。相当于removeFirst public boolean isEmpty():如果列表不包含元素，则返回true详细：从源码角度认识ArrayList，LinkedList与HashMap2.3.4.3 set()和get()函数public E get(int index) { checkElementIndex(index); return node(index).item; } public E set(int index, E element) { checkElementIndex(index); Node<E> x = node(index); E oldVal = x.item; x.item = element; return oldVal; }首先还是检查index，接下来都调用了node(index);下面是这个函数的实现：/** * Returns the (non-null) Node at the specified element index. */ Node<E> node(int index) { // assert isElementIndex(index); if (index < (size >> 1)) { Node<E> x = first; for (int i = 0; i < index; i++) x = x.next; return x; } else { Node<E> x = last; for (int i = size - 1; i > index; i--) x = x.prev; return x; } }该函数会以O(n/2)的性能去获取一个节点，就是判断index是在前半区间还是后半区间，如果在前半区间就从head搜索，而在后半区间就从tail搜索。而不是一直从头到尾的搜索。如此设计，将节点访问的复杂度由O(n)变为O(n/2)。2.4 Queue集合2.4.1 概况Queue用户模拟队列这种数据结构，队列通常是指“先进先出”(FIFO，first-in-first-out)的容器。队列的头部是在队列中存放时间最长的元素，队列的尾部是保存在队列中存放时间最短的元素。新元素插入（offer）到队列的尾部，访问元素（poll）操作会返回队列头部的元素。通常，队列不允许随机访问队列中的元素。2.4.2 接口方法3 Map接口详解3.1 概括Map用户保存具有映射关系的数据，因此Map集合里保存着两组数，一组值用户保存Map里的key,另一组值用户保存Map里的value，key和value都可以是任何引用类型的数据。Map的key不允许重复，即同一个Map对象的任何两个key通过equals方法比较总是返回false。key和value之间存在单向一对一关系，即通过指定的key,总能找到唯一的、确定的value。从Map中取出数据时，只要给出指定的key，就可以取出对应的value。常用的Map继承关系图，图片转载自参考6：3.2 Map与Set集合、List集合的关系① 与Set集合的关系如果把Map里的所有key放在一起看，它们就组成了一个Set集合（所有的key没有顺序，key与key之间不能重复），实际上Map确实包含了一个keySet()方法，用户返回Map里所有key组成的Set集合。② 与List集合的关系如果把Map里的所有value放在一起来看，它们又非常类似于一个List：元素与元素之间可以重复，每个元素可以根据索引来查找，只是Map中索引不再使用整数值，而是以另外一个对象作为索引。3.3 接口方法Map中还有一个内部类Entry，该类封装了一个key-value对。Entry包含如下三个方法：3.4 HashMap3.4.1 概括HashMap<K, V>是基于哈希表这个数据结构的Map接口具体实现，允许null键和null值（最多只允许一个key为null，但允许多个value为null）。这个类与HashTable近似等价，区别在于HashMap不是线程安全的并且允许null键和null值。由于基于哈希表实现，所以HashMap内部的元素是无序的。HashMap对与get与put操作的时间复杂度是常数级别的（在散列均匀的前提下）。对HashMap的集合视图进行迭代所需时间与HashMap的capacity（bucket的数量）加上HashMap的尺寸（键值对的数量）成正比。因此，若迭代操作的性能很重要，不要把初始capacity设的过高（不要把load factor设的过低）。HashMap底层实现是数组 + 链表 + 红黑树（JDK1.8增加红黑树部分），当链表长度超过阈值（8）,时，将链表转换为红黑树，这样大大减少了查找时间。不懂散列表（哈希表 Hash Table）戳这里 散列表的原理与实现更加详细源码解刨 戳这里 从源码角度认识ArrayList，LinkedList与HashMapHashMap是一个Android开发或者Java开发者必须掌握的知识点。HashMap在中高岗位面试题常有它的身影。例如：HashMap 和 HashTable 以及 CurrentHashMap（ConcurrentHashMap） 的区别。哈希碰撞，哈希计算，哈希映射，为什么是头插法，扩容为什么是 2 的幂次等这样的问题。3.4.2 capacity和load factorcapacity是容量，load factor是负载因子（默认是0.75）简单的说，Capacity就是bucket的大小，Load factor就是bucket填满程度的最大比例。如果对迭代性能要求很高的话，不要把capacity设置过大，也不要把loadfactor设置过小。当bucket中的entries的数目大于capacity*load factor时就需要调整bucket的大小为当前的2倍。3.4.3 HashMap底层详解HashMap底层实现是位桶bucket（数组） + 链表 + 红黑树（JDK1.8增加红黑树部分）。HashMap是一个用于存储Key-Value键值对的集合，每一个键值对也叫作Entry，这些键值对分散存储在一个数组当中，这个数值就是HashMap的主干。下面对源码进行剖析： /* ---------------- Fields -------------- */ /** * The table, initialized on first use, and resized as * necessary. When allocated, length is always a power of two. * (We also tolerate length zero in some operations to allow * bootstrapping mechanics that are currently not needed.) * 底层数组，充当哈希表的作用，用于存储对应hash位置的元素Node<K,V>，此数组长度总是2的N次幂。 * * */ transient Node<K,V>[] table; /** * Holds cached entrySet(). Note that AbstractMap fields are used * for keySet() and values(). * */ transient Set<Map.Entry<K,V>> entrySet; /** * The number of key-value mappings contained in this map. * 实际存储的key - value 键值对 个数 */ transient int size; /** * The number of times this HashMap has been structurally modified * Structural modifications are those that change the number of mappings in * the HashMap or otherwise modify its internal structure (e.g., * rehash). This field is used to make iterators on Collection-views of * the HashMap fail-fast. (See ConcurrentModificationException). * * */ transient int modCount; /** * The next size value at which to resize (capacity * load factor). * 下一次扩容时的阈值，达到阈值便会触发扩容机制resize * (阈值 threshold = 容器容量 capacity * 负载因子 load factor). * * @serial */ // (The javadoc description is true upon serialization. // Additionally, if the table array has not been allocated, this // field holds the initial array capacity, or zero signifying // DEFAULT_INITIAL_CAPACITY.) int threshold; /** * The load factor for the hash table. * 哈希表的负载因子，默认0.75 * * @serial */ final float loadFactor;Node<K,V>[] table 中Node<K,V>详解： /** * Basic hash bin node, used for most entries. (See below for * TreeNode subclass, and in LinkedHashMap for its Entry subclass.) * 定义HashMap存储元素结点的底层实现 */ static class Node<K,V> implements Map.Entry<K,V> { final int hash; // 元素的哈希值 由final修饰可知，当hash的值确定后，就不能再修改 final K key; // 键，由final修饰可知，当key的值确定后，就不能再修改 V value; // 值 Node<K,V> next; // 记录下一个元素节点（单链表结构，用于解决hash冲突，后面会讲到hash冲突） /** * Node结点构造方法 */ Node(int hash, K key, V value, Node<K,V> next) { this.hash = hash; // 元素的哈希值 this.key = key; // 键 this.value = value; // 值 this.next = next; // 记录下一个元素结点 } public final K getKey() { return key; } public final V getValue() { return value; } public final String toString() { return key + "=" + value; } /** * 为Node重写hashCode方法，值为：key的hashCode 异或 value的hashCode * 运算作用就是将2个hashCode的二进制中，同一位置相同的值为0，不同的为1。 */ public final int hashCode() { return Objects.hashCode(key) ^ Objects.hashCode(value); } /** * 修改某一元素的值 */ public final V setValue(V newValue) { V oldValue = value; value = newValue; return oldValue; } /** * 为Node重写equals方法 */ public final boolean equals(Object o) { if (o == this) return true; if (o instanceof Map.Entry) { Map.Entry<?,?> e = (Map.Entry<?,?>)o; if (Objects.equals(key, e.getKey()) && Objects.equals(value, e.getValue())) return true; } return false; } }hashMap内存结构图 - 图片来自于《美团点评技术团队文章》：3.4.4 put函数调用put(K key, V value)操作添加key-value键值对时，进行了如下操作：1. 判断哈希表Node<K,V>[] table是否为空或者null，是则执行resize()方法进行扩容初始化。2. 对key的hashCode()做hash，然后再计算index;index计算：通过(n - 1) & hash当前元素的hash值 & hash表长度 - 1（实际就是 hash值 % hash表长度） 计算出存储位置table[i]。如果存储位置没有元素存放，则将新增结点存储在此位置table[i]。3. 如果存储位置有元素存放，则判断该位置已有的hash和key是否和当前操作的元素一致，一致覆盖，不一致则table[i]位置发生了hash冲突（碰撞）。4. 如果发生hash冲突（碰撞），首先通过判断头结点是否是treeNode，如果是treeNode则证明此位置的结构是红黑树，就使用红黑树的方式新增结点。如果不是treeNode则证明是单链表结构，将新增结点插入至链表的最后位置，随后判断链表长度是否大于8，是则将当前存储位置的链表转化为红黑树（JDK1.8），遍历过程中如果发现hash和key已经存在，则直接覆盖value。5. 插入成功后，判断当前存储键值对的数量 （size）大于 阈值threshold 是则扩容。threshold等于capacity*load factor。hashMap put方法执行流程图- 图片来自于《美团点评技术团队文章》：源码解析： /** * 添加key-value键值对 * * @param key 键 * @param value 值 * @return 如果原本存在此key，则返回旧的value值，如果是新增的key- value，则返回nulll * * Associates the specified value with the specified key in this map. * If the map previously contained a mapping for the key, the old * value is replaced. * * @param key key with which the specified value is to be associated * @param value value to be associated with the specified key * @return the previous value associated with <tt>key</tt>, or * <tt>null</tt> if there was no mapping for <tt>key</tt>. * (A <tt>null</tt> return can also indicate that the map * previously associated <tt>null</tt> with <tt>key</tt>.) */ public V put(K key, V value) { // 对key的hashCode()做hash return putVal(hash(key), key, value, false, true); } /** * Implements Map.put and related methods * * @param hash hash for key * @param key the key * @param value the value to put * @param onlyIfAbsent if true, don't change existing value * @param evict if false, the table is in creation mode. * @return previous value, or null if none */ /** * 添加key-value键值对的实际调用方法（重点） * * @param hash key 键的hash值 * @param key 键 * @param value 值 * @param onlyIfAbsent 此值如果是true, 则如果此key已存在value，则不执 * 行修改操作 * @param evict 此值如果是false，哈希表是在初始化模式 * @return 返回原本的旧值, 如果是新增，则返回null */ final V putVal(int hash, K key, V value, boolean onlyIfAbsent, boolean evict) { // 用于记录当前的hash表 Node<K,V>[] tab; // 用于记录当前的链表结点 Node<K,V> p; // n用于记录hash表的长度，i用于记录当前操作索引index int n, i; // tab为空则创建（当前hash表为空） if ((tab = table) == null || (n = tab.length) == 0) // 初始化hash表，并把初始化后的hash表长度值赋值给n n = (tab = resize()).length; // 计算index，并对null做处理 // 1）通过 (n - 1) & hash 当前元素的hash值 & hash表长度 - 1 // 2）确定当前元素的存储位置，此运算等价于 当前元素的hash值 % hash表的长度 // 3）计算出的存储位置没有元素存在 if ((p = tab[i = (n - 1) & hash]) == null) // 4) 则新建一个Node结点，在该位置存储此元素 tab[i] = newNode(hash, key, value, null); else { // 当前存储位置已经有元素存在了(不考虑是修改的情况的话，就代表发生hash冲突了) // 用于存放新增结点 Node<K,V> e; // 用于临时存在某个key值 K k; // 结点存在 // 1)如果当前位置已存在元素的hash值和新增元素的hash值相等 // 2)并且key也相等，则证明是同一个key元素，想执行修改value操作 if (p.hash == hash && ((k = p.key) == key || (key != null && key.equals(k)))) e = p;// 将当前结点引用赋值给e // 当前结点为红黑树 else if (p instanceof TreeNode) // 则证明当前位置的链表已变成红黑树结构，则已红黑树结点结构新增元素 e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value); // 排除上述情况，则证明已发生hash冲突，并hash冲突位置现时的结构是单链表结构 else { for (int binCount = 0; ; ++binCount) { //遍历单链表，将新元素结点放置此链表的最后一位 if ((e = p.next) == null) { // 将新元素结点放在此链表的最后一位 p.next = newNode(hash, key, value, null); // 新增结点后，当前结点数量是否大于等于 阈值 8 if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st // 大于等于8则将链表转换成红黑树 treeifyBin(tab, hash); break; } // 如果链表中已经存在对应的key，则覆盖value if (e.hash == hash && ((k = e.key) == key || (key != null && key.equals(k)))) break; p = e; } } // 写入 if (e != null) { // existing mapping for key V oldValue = e.value; // 如果允许修改，则修改value为新值 if (!onlyIfAbsent || oldValue == null) e.value = value; afterNodeAccess(e); return oldValue; } } ++modCount; // 当前存储键值对的数量 大于 阈值 是则扩容 if (++size > threshold) // 重置hash大小，将旧hash表的数据逐一复制到新的hash表中（后面详细讲解） resize(); afterNodeInsertion(evict); // 返回null，则证明是新增操作，而不是修改操作 return null; }3.4.5 get函数调用get(Object key)操作根据键key查找对应的key-value键值对时，进行了如下操作：1. 先调用 hash(key)方法计算出 key 的 hash值。2. 根据查找的键值key的hash值，通过(n - 1) & hash当前元素的hash值 & hash表长度 - 1（实际就是 hash值 % hash表长度）计算出存储位置table[i]，判断存储位置是否有元素存在 。如果存储位置有元素存放，则首先比较头结点元素，如果头结点的key的hash值和要获取的key的hash值相等，并且头结点的key本身 和要获取的 key 相等，则返回该位置的头结点。如果存储位置没有元素存放，则返回null。3. 如果存储位置有元素存放，但是头结点元素不是要查找的元素，则需要遍历该位置进行查找。4. 先判断头结点是否是treeNode，如果是treeNode则证明此位置的结构是红黑树，以红色树的方式遍历查找该结点，没有则返回null。5. 如果不是treeNode，则证明是单链表，遍历单链表，逐一比较链表结点，链表结点的key的hash值 和 要获取的key的hash值相等，并且链表结点的key本身和要获取的 key 相等，则返回该结点，遍历结束仍未找到对应key的结点，则返回null。源码分析： /** * 返回指定 key 所映射的 value 值 * 或者 返回 null 如果容器里不存在对应的key * * 更确切地讲，如果此映射包含一个满足 (key==null ? k==null :key.equals(k)) * 的从 k 键到 v 值的映射关系， * 则此方法返回 v；否则返回 null。（最多只能有一个这样的映射关系。） * * 返回 null 值并不一定 表明该映射不包含该键的映射关系； * 也可能该映射将该键显示地映射为 null。可使用containsKey操作来区分这两种情况。 * * @see #put(Object, Object) */ public V get(Object key) { Node<K,V> e; // 1.先调用 hash(key)方法计算出 key 的 hash值 // 2.随后调用getNode方法获取对应key所映射的value值 return (e = getNode(hash(key), key)) == null ? null : e.value; } /** * 获取哈希表结点的方法实现 * * @param hash key 键的hash值 * @param key 键 * @return 返回对应的结点，如果结点不存在，则返回null */ final Node<K,V> getNode(int hash, Object key) { // 用于记录当前的hash表 Node<K,V>[] tab; // first用于记录对应hash位置的第一个结点，e充当工作结点的作用 Node<K,V> first, e; // n用于记录hash表的长度 int n; // 用于临时存放Key K k; // 通过 (n - 1) & hash 当前元素的hash值 & hash表长度 - 1 // 判断当前元素的存储位置是否有元素存在 if ((tab = table) != null && (n = tab.length) > 0 && (first = tab[(n - 1) & hash]) != null) {//元素存在的情况 // 如果头结点的key的hash值 和 要获取的key的hash值相等 // 并且 头结点的key本身 和要获取的 key 相等 if (first.hash == hash && // always check first node 总是检查头结点 ((k = first.key) == key || (key != null && key.equals(k)))) // 返回该位置的头结点 return first; if ((e = first.next) != null) {// 头结点不相等 if (first instanceof TreeNode) // 如果当前结点是树结点 // 则证明当前位置的链表已变成红黑树结构 // 通过红黑树结点的方式获取对应key结点 return ((TreeNode<K,V>)first).getTreeNode(hash, key); do {// 当前位置不是红黑树，则证明是单链表 // 遍历单链表，逐一比较链表结点 // 链表结点的key的hash值 和 要获取的key的hash值相等 // 并且 链表结点的key本身 和要获取的 key 相等 if (e.hash == hash && ((k = e.key) == key || (key != null && key.equals(k)))) // 找到对应的结点则返回 return e; } while ((e = e.next) != null); } } // 通过上述查找均无找到，则返回null return null; }3.4.6 remove函数调用remove(Object key)操作根据键key删除对应的key-value键值对时，进行了如下操作：1. 先调用 hash(key)方法计算出 key 的 hash值。2. 根据查找的键值key的hash值，通过(n - 1) & hash当前元素的hash值 & hash表长度 - 1（实际就是 hash值 % hash表长度）计算出存储位置table[i]，判断存储位置是否有元素存在 。如果存储位置有元素存放，则首先比较头结点元素，如果头结点的key的hash值和要获取的key的hash值相等，并且头结点的key本身和要获取的 key 相等，则该位置的头结点即为要删除的结点，记录此结点至变量node中。如果存储位置没有元素存放，则返回null。3. 如果存储位置有元素存放，但是头结点元素不是要删除的元素，则需要遍历该位置进行查找。4. 先判断头结点是否是treeNode，如果是treeNode则证明此位置的结构是红黑树，以红色树的方式遍历查找并删除该结点，没有则返回null。5. 如果不是treeNode，则证明是单链表，遍历单链表，逐一比较链表结点，链表结点的key的hash值 和 要获取的key的hash值相等，并且链表结点的key本身和要获取的 key 相等，则此为要删除的结点，记录此结点至变量node中，遍历结束仍未找到对应key的结点，则返回null。6. 如果找到要删除的结点node，则判断是否需要比较value也是否一致，如果value值一致或者不需要比较value值，则执行删除结点操作，删除操作根据不同的情况与结构进行不同的处理。如果当前结点是树结点，则证明当前位置的链表已变成红黑树结构，通过红黑树结点的方式删除对应结点。如果不是红黑树，则证明是单链表。如果要删除的是头结点，则当前存储位置table[i]的头结点指向删除结点的下一个结点。如果要删除的结点不是头结点，则将要删除的结点的后继结点node.next赋值给要删除结点的前驱结点的next域，即p.next = node.next;。7. HashMap当前存储键值对的数量 - 1，并返回删除结点。源码分析： /** * 从此映射中移除指定键的映射关系（如果存在）。 * * @param key 其映射关系要从映射中移除的键 * @return 与 key 关联的旧值；如果 key 没有任何映射关系，则返回 null。 * （返回 null 还可能表示该映射之前将 null 与 key 关联。） */ public V remove(Object key) { Node<K,V> e; // 1.先调用 hash(key)方法计算出 key 的 hash值 // 2.随后调用removeNode方法删除对应key所映射的结点 return (e = removeNode(hash(key), key, null, false, true)) == null ? null : e.value; } /** * 删除哈希表结点的方法实现 * * @param hash 键的hash值 * @param key 键 * @param value 用于比较的value值，当matchValue 是 true时才有效, 否则忽略 * @param matchValue 如果是 true 只有当value相等时才会移除 * @param movable 如果是 false当执行移除操作时，不删除其他结点 * @return 返回删除结点node，不存在则返回null */ final Node<K,V> removeNode(int hash, Object key, Object value, boolean matchValue, boolean movable) { // 用于记录当前的hash表 Node<K,V>[] tab; // 用于记录当前的链表结点 Node<K,V> p; // n用于记录hash表的长度，index用于记录当前操作索引index int n, index; // 通过 (n - 1) & hash 当前元素的hash值 & hash表长度 - 1 // 判断当前元素的存储位置是否有元素存在 if ((tab = table) != null && (n = tab.length) > 0 && (p = tab[index = (n - 1) & hash]) != null) {// 元素存在的情况 // node 用于记录找到的结点，e为工作结点 Node<K,V> node = null, e; K k; V v; // 如果头结点的key的hash值 和 要获取的key的hash值相等 // 并且 头结点的key本身 和要获取的 key 相等 // 则证明此头结点就是要删除的结点 if (p.hash == hash && ((k = p.key) == key || (key != null && key.equals(k)))) // 记录要删除的结点的引用地址至node中 node = p; else if ((e = p.next) != null) {// 头结点不相等 if (p instanceof TreeNode)// 如果当前结点是树结点 // 则证明当前位置的链表已变成红黑树结构 // 通过红黑树结点的方式获取对应key结点 // 记录要删除的结点的引用地址至node中 node = ((TreeNode<K,V>)p).getTreeNode(hash, key); else {// 当前位置不是红黑树，则证明是单链表 do { // 遍历单链表，逐一比较链表结点 // 链表结点的key的hash值 和 要获取的key的hash值相等 // 并且 链表结点的key本身 和要获取的 key 相等 if (e.hash == hash && ((k = e.key) == key || (key != null && key.equals(k)))) { // 找到则记录要删除的结点的引用地址至node中，中断遍历 node = e; break; } p = e; } while ((e = e.next) != null); } } // 如果找到要删除的结点，则判断是否需要比较value也是否一致 if (node != null && (!matchValue || (v = node.value) == value || (value != null && value.equals(v)))) { // value值一致或者不需要比较value值，则执行删除结点操作 if (node instanceof TreeNode) // 如果当前结点是树结点 // 则证明当前位置的链表已变成红黑树结构 // 通过红黑树结点的方式删除对应结点 ((TreeNode<K,V>)node).removeTreeNode(this, tab, movable); else if (node == p) // node 和 p相等，则证明删除的是头结点 // 当前存储位置的头结点指向删除结点的下一个结点 tab[index] = node.next; else // 删除的不是头结点 // p是删除结点node的前驱结点，p的next改为记录要删除结点node的后继结点 p.next = node.next; ++modCount; // 当前存储键值对的数量 - 1 --size; afterNodeRemoval(node); // 返回删除结点 return node; } } // 不存在要删除的结点，则返回null return null; }3.4.7 replace函数调用replace(K key, V value)操作根据键key查找对应的key-value键值对，随后替换对应的值value，进行了如下操作：1. 先调用 hash(key)方法计算出 key 的 hash值。2. 随后调用getNode方法获取对应key所映射的value值 。3. 记录元素旧值，将新值赋值给元素，返回元素旧值，如果没有找到元素，则返回null。源码分析： /** * 替换指定 key 所映射的 value 值 * * @param key 对应要替换value值元素的key键 * @param value 要替换对应元素的新value值 * @return 返回原本的旧值，如果没有找到key对应的元素，则返回null * @since 1.8 JDK1.8新增方法 */ public V replace(K key, V value) { Node<K,V> e; // 1.先调用 hash(key)方法计算出 key 的 hash值 // 2.随后调用getNode方法获取对应key所映射的value值 if ((e = getNode(hash(key), key)) != null) {// 如果找到对应的元素 // 元素旧值 V oldValue = e.value; // 将新值赋值给元素 e.value = value; afterNodeAccess(e); // 返回元素旧值 return oldValue; } // 没有找到元素，则返回null return null; }3.4.8 hash计算在get和put的过程中，计算下标时，先对hashCode进行hash操作，然后再通过hash值进一步计算下标，如下图所示：源码分析：/** * JDK 7 的 hash方法 */ final int hash(int h) { h ^= k.hashCode(); h ^= (h >>> 20) ^ (h >>> 12); return h ^ (h >>> 7) ^ (h >>> 4); } /** * JDK 8 的 hash方法 * 根据key 键 的 hashCode 通过 “扰动函数” 生成对应的 hash值 * 经过此操作后，使每一个key对应的hash值生成的更均匀， * 减少元素之间的碰撞几率（后面详细说明） */ static final int hash(Object key) { int h; return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16); JDK7：做了4次16位右位移异或混合JDK8：可以看到这个函数大概的作用就是：高16bit不变，低16bit和高16bit做了一个异或。在设计hash函数时，因为目前的table长度n为2的幂，而计算下标的时候，是这样实现的(使用&位操作，而非%求余)：(n - 1) & hash设计者认为这方法很容易发生碰撞。为什么这么说呢？不妨思考一下，在n - 1为15(0x1111)时，其实散列真正生效的只是低4bit的有效位，当然容易碰撞了。因此，设计者想了一个顾全大局的方法(综合考虑了速度、作用、质量)，就是把高16bit和低16bit异或了一下。设计者还解释到因为现在大多数的hashCode的分布已经很不错了，就算是发生了碰撞也用O(logn)的tree去做了。仅仅异或一下，既减少了系统的开销，也不会造成的因为高位没有参与下标的计算(table长度比较小时)，从而引起的碰撞。在Java 8之前的实现中是用链表解决冲突的，在产生碰撞的情况下，进行get时，两步的时间复杂度是O(1)+O(n)。因此，当碰撞很厉害的时候n很大，O(n)的速度显然是影响速度的。因此在Java 8中，利用红黑树替换链表（当存在位置的链表长度 大于等于 8 时），这样复杂度就变成了O(1)+O(logn)了，这样在n很大的时候，能够比较理想的解决这个问题。3.4.9 resize函数构造hash表时，如果不指明初始大小，默认大小为16（即Node数组大小16）。当put时，当发现目前的bucket占用程度已经超过Load Factor比例，就会执行resize()，在resize的过程中，会把bucket进行2次幂的扩展(指长度扩为原来2倍)，元素的位置要么是在原位置，要么是在原位置再移动2次幂的位置。（耗时）16扩充到32时，具体的变化如下图所示：因此元素在重新获取hash之后，因为n变为2倍，那么n-1的mask范围在高位多1bit(红色)，因此新的index就会发生这样的变化：因此，我们在扩充HashMap的时候，不需要重新计算hash，只需要看看原来的hash值新增的那个bit是1还是0就好了，是0的话索引没变，是1的话索引变成“原索引+oldCap”。可以看看下图为16扩充为32的resize示意图：这个设计确实非常的巧妙，既省去了重新计算hash值的时间，而且同时，由于新增的1bit是0还是1可以认为是随机的，因此resize的过程，均匀的把之前的冲突的节点分散到新的bucket了。源码分析： final Node<K,V>[] resize() { Node<K,V>[] oldTab = table; int oldCap = (oldTab == null) ? 0 : oldTab.length; int oldThr = threshold; int newCap, newThr = 0; // 如果旧表的长度不是空 if (oldCap > 0) { // 超过最大值就不再扩充了 if (oldCap >= MAXIMUM_CAPACITY) { threshold = Integer.MAX_VALUE; return oldTab; } // 没超过最大值，就扩充为原来的2倍 else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY && oldCap >= DEFAULT_INITIAL_CAPACITY) // 把新表的门限设置为旧表门限的两倍 newThr = oldThr << 1; // double threshold } // 如果旧表的长度的是0，就是说第一次初始化表 else if (oldThr > 0) // initial capacity was placed in threshold newCap = oldThr; else { // zero initial threshold signifies using defaults newCap = DEFAULT_INITIAL_CAPACITY; newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY); } // 计算新的resize上限 if (newThr == 0) { // 新表长度乘以加载因子 float ft = (float)newCap * loadFactor; newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ? (int)ft : Integer.MAX_VALUE); } threshold = newThr; @SuppressWarnings({"rawtypes","unchecked"}) // 下面开始构造新表，初始化表中的数据 Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap]; table = newTab; //把新表赋值给table if (oldTab != null) { // 遍历原来的旧表，把每个bucket都移动到新的buckets中 for (int j = 0; j < oldCap; ++j) { Node<K,V> e; if ((e = oldTab[j]) != null) { oldTab[j] = null; // 说明这个node没有链表直接放在新表的e.hash & (newCap - 1)位置 if (e.next == null) newTab[e.hash & (newCap - 1)] = e; else if (e instanceof TreeNode) ((TreeNode<K,V>)e).split(this, newTab, j, oldCap); else { // preserve order Node<K,V> loHead = null, loTail = null; Node<K,V> hiHead = null, hiTail = null; Node<K,V> next; do { next = e.next; // 原索引 if ((e.hash & oldCap) == 0) { if (loTail == null) loHead = e; else loTail.next = e; loTail = e; } // 原索引+oldCap else { if (hiTail == null) hiHead = e; else hiTail.next = e; hiTail = e; } } while ((e = next) != null); // 原索引放到bucket里 if (loTail != null) { loTail.next = null; newTab[j] = loHead; } // 原索引+oldCap放到bucket里 if (hiTail != null) { hiTail.next = null; newTab[j + oldCap] = hiHead; } } } } } return newTab; }3.4.10 HashMap线程安全性HashMap不是线程安全的，如果多个线程同时对同一个HashMap更改数据的话，会导致数据不一致或者数据污染。如果出现线程不安全的操作时，HashMap会尽可能的抛出ConcurrentModificationException防止数据异常，当我们在对一个HashMap进行遍历时，在遍历期间，我们是不能对HashMap进行添加，删除等更改数据的操作的，否则也会抛出ConcurrentModificationException异常，此为fail-fast（快速失败）机制。从源码上分析，我们在put,remove等更改HashMap数据时，都会导致modCount的改变，当expectedModCount != modCount时，则抛出ConcurrentModificationException。如果想要线程安全，可以考虑使用ConcurrentHashMap。而且，在多线程下操作HashMap，由于存在扩容机制，当HashMap调用resize()进行自动扩容时，可能会导致死循环的发生。HashMap的线程不安全主要体现在下面两个方面：1.在JDK1.7中，当并发执行扩容操作时会造成环形链和数据丢失的情况。2.在JDK1.8中，在并发执行put操作时会发生数据覆盖的情况。详情参考：HashMap头插法的危害头差法危害 引用倒转 多线程死循环3.4.11 HashMap的容量一定是2的n次方1. 因为调用put(K key, V value)操作添加key-value键值对时，具体确定此元素的位置是通过hash值 % 模上 哈希表Node<K,V>[] table的长度hash%length 计算的。但是"模"运算的消耗相对较大，通过位运算h&(length-1)也可以得到取模后的存放位置，而位运算的运行效率高，但只有length的长度是2的n次方时，h&(length-1)才等价于h%length。2. 而且当数组长度为2的n次幂的时候，不同的key算出的index相同的几率较小，那么数据在数组上分布就比较均匀，也就是说碰撞的几率小，相对的，查询的时候就不用遍历某个位置上的链表，这样查询效率也就较高了。3. 不浪费空间。 上图中，左边两组的数组长度是16（2的4次方），右边两组的数组长度是15。两组的hash值均为8和9。1. 当数组长度是15时，当它们和1110进行&与运算（相同为1，不同为0）时，计算的结果都是1000，所以他们都会存放在相同的位置table[8]中，这样就发生了hash冲突，那么查询时就要遍历链表，逐一比较hash值，降低了查询的效率。2. 当数组长度为15的时候，hashcode的值会与14（1110）进行“与”，那么最后一位永远是0，而0001，0011，0101，1001，1011，0111，1101这几个位置永远都不能存放元素了，空间浪费相当大，更糟的是这种情况中，数组可以使用的位置比数组长度小了很多，这意味着进一步增加了碰撞的几率，减慢了查询的效率！3.4.12 红黑树工作原理：前面产生冲突的那些KEY对应的记录只是简单的追加到一个链表后面，这些记录只能通过遍历来进行查找。但是超过这个阈值后HashMap开始将列表升级成一个二叉树，使用哈希值作为树的分支变量，如果两个哈希值不等，但指向同一个桶的话，较大的那个会插入到右子树里。如果哈希值相等，HashMap希望key值最好是实现了Comparable接口的，这样它可以按照顺序来进行插入。源码解析：//红黑树 static final class TreeNode<k,v> extends LinkedHashMap.Entry<k,v> { TreeNode<k,v> parent; // 父节点 TreeNode<k,v> left; //左子树 TreeNode<k,v> right;//右子树 TreeNode<k,v> prev; // needed to unlink next upon deletion boolean red; //颜色属性 TreeNode(int hash, K key, V val, Node<k,v> next) { super(hash, key, val, next); } //返回当前节点的根节点 final TreeNode<k,v> root() { for (TreeNode<k,v> r = this, p;;) { if ((p = r.parent) == null) return r; r = p; } } }3.4.13 HashMap总结1. HashMap是基于Map接口实现的一种键-值对<key,value>的存储结构，允许null值，同时非有序，非同步(即线程不安全)。HashMap的底层实现是数组 + 链表 + 红黑树（JDK1.8增加了红黑树部分）。2. HashMap定位元素位置是通过键key经过扰动函数扰动后得到hash值，然后再通过hash & (length - 1)代替取模的方式进行元素定位的。3. hash的实现的原理：在Java 1.8的实现中，是通过hashCode()的高16位异或低16位实现的：(h =k.hashCode()) ^ (h >>> 16)，主要是从速度、功效、质量来考虑的，这么做可以在bucket的n比较小的时候，也能保证考虑到高低bit都参与到hash的计算中，同时不会有太大的开销。4. HashMap是使用链地址法（拉链法，拉链哈希）解决hash冲突的，当有冲突元素放进来时，会将此元素插入至此位置链表的最后一位，形成单链表。当存在位置的链表长度 大于等于 8 时，HashMap会将链表转变为红黑树，以此提高查找效率。5. HashMap的容量是2的n次方，有利于提高计算元素存放位置时的效率，也降低了hash冲突的几率。因此，我们使用HashMap存储大量数据的时候，最好先预先指定容器的大小为2的n次方，即使我们不指定为2的n次方，HashMap也会把容器的大小设置成最接近设置数的2的n次方。如：设置HashMap的大小为7 ，则HashMap会将容器大小设置成最接近7的一个2的n次方数，此值为8 。6. HashMap的负载因子表示哈希表空间的使用程度（或者说是哈希表空间的利用率）。当负载因子越大，则HashMap的装载程度就越高。也就是能容纳更多的元素，元素多了，发生hash碰撞的几率就会加大，从而链表就会拉长，此时的查询效率就会降低。当负载因子越小，则链表中的数据量就越稀疏，此时会对空间造成浪费，但是此时查询效率高。7. HashMap不是线程安全的，Hashtable则是线程安全的。但Hashtable是一个遗留容器，如果我们不需要线程同步，则建议使用HashMap，如果需要线程同步，则建议使用ConcurrentHashMap。8. 在多线程下操作HashMap，由于存在扩容机制，当HashMap调用resize()进行自动扩容时，可能会导致死循环的发生。9. 我们在使用HashMap时，最好选择不可变对象作为key。例如String，Integer等不可变类型作为key。如果key对象是可变的，那么key的哈希值就可能改变。在HashMap中可变对象作为Key会造成数据丢失。因为我们再进行hash & (length - 1)取模运算计算位置查找对应元素时，位置可能已经发生改变，导致数据丢失。10. JDK1.7的hash碰撞采用头插法，JDK1.8则是尾插法，配合红黑树。11. JDK1.7中是先扩容后插入新值的，JDK1.8中是先插值再扩容。12. 链表长度达到 8 就转成红黑树，而当长度降到 6 就转换回去，这体现了时间和空间平衡的思想，最开始使用链表的时候，空间占用是比较少的，而且由于链表短，所以查询时间也没有太大的问题。可是当链表越来越长，需要用红黑树的形式来保证查询的效率。3.5 ConcurrentHashMap3.5.1 概括因为多线程环境下，使用HashMap进行put操作可能会线程不安全，所以在并发情况下不能使用HashMap。而HashTable线程安全，但是效率低。所以就有了ConcurrentHashMap。ConcurrentHashMap 是一个并发散列映射表，它允许完全并发的读取，并且支持给定数量的并发更新。Hashtable容器使用synchronized来保证线程安全（方法级别阻塞），但在线程竞争激烈的情况下Hashtable的效率非常低下。因为当一个线程访问Hashtable的同步方法时，其他线程访问Hashtable的同步方法时，可能会进入阻塞或轮询状态。它们占用共享资源锁，所以导致同时只能一个线程操作 get 或者 put ，而且 get/put 操作不能同时执行，所以这种同步的集合效率非常低。如线程1使用put进行添加元素，线程2不但不能使用put方法添加元素，并且也不能使用get方法来获取元素，所以竞争越激烈效率越低。解决思路：JDK1.7：HashTable容器在竞争激烈的并发环境下表现出效率低下的原因，是因为所有访问HashTable的线程都必须竞争同一把锁，那假如容器里有多把锁，每一把锁用于锁容器其中一部分数据，那么当多线程访问容器里不同数据段的数据时，线程间就不会存在锁竞争，从而可以有效的提高并发访问效率，这就是ConcurrentHashMap所使用的锁分段技术，首先将数据分成一段一段的存储，然后给每一段数据配一把锁，当一个线程占用锁访问其中一个段数据的时候，其他段的数据也能被其他线程访问。有些方法需要跨段，比如size()和containsValue()，它们可能需要锁定整个表而而不仅仅是某个段，这需要按顺序锁定所有段，操作完毕后，又按顺序释放所有段的锁。这里“按顺序”是很重要的，否则极有可能出现死锁，在ConcurrentHashMap内部，段数组是final的，并且其成员变量实际上也是final的，但是，仅仅是将数组声明为final的并不保证数组成员也是final的，这需要实现上的保证。这可以确保不会出现死锁，因为获得锁的顺序是固定的。ConcurrentHashMap是由Segment数组结构和HashEntry数组结构组成。Segment是一种可重入锁ReentrantLock，在ConcurrentHashMap里扮演锁的角色，HashEntry则用于存储键值对数据。一个ConcurrentHashMap里包含一个Segment数组，Segment的结构和HashMap类似，是一种数组和链表结构， 一个Segment里包含一个HashEntry数组，每个HashEntry是一个链表结构的元素， 每个Segment守护者一个HashEntry数组里的元素,当对HashEntry数组的数据进行修改时，必须首先获得它对应的Segment锁。（使用分段加锁的一个方式，分成16个桶，每次只加锁其中一个桶）JDK1.8：抛弃了Segment分段锁机制，并发控制使用CAS+Synchronized来保证并发更新的安全。数据结构采用：Node数组+链表+红黑树，虽然在JDK1.8中还能看到Segment的数据结构，但是已经简化了属性，只是为了兼容旧版本。1. table：默认为null，初始化发生在第一次插入操作，默认大小为16的数组，用来存储Node节点数据，扩容时大小总是2的幂次方。2. nextTable：默认为null，扩容时新生成的数组，其大小为原数组的两倍。3. sizeCtl：默认为0，用来控制table的初始化和扩容操作，具体应用在后续会体现出来。当为负值时，表将被初始化或调整大小:-1表示初始化，否则-(1 +活动调整大小的线程数)。否则，当表为空时，保留创建时使用的初始表大小，默认为0。初始化之后，保存下一个元素count值，根据该值调整表的大小。4. Node：保存key，value及key的hash值的数据结构。其中value和next都用volatile修饰，保证并发的可见性。5. ForwardingNode：一个特殊的Node节点，hash值为-1，其中存储nextTable的引用。只有table发生扩容的时候，ForwardingNode才会发挥作用，作为一个占位符放在table中表示当前节点为null或则已经被移动。3.5.2 结构基础分析put、get等方法源码前，先了解一下ConcurrentHashMap常量设计和数据结构。3.5.2.1 常量// node数组最大容量：2^30=1073741824 private static final int MAXIMUM_CAPACITY = 1 << 30; // 默认初始值，必须是2的幕数 private static final int DEFAULT_CAPACITY = 16; //数组可能最大值，需要与toArray（）相关方法关联 static final int MAX_ARRAY_SIZE = Integer.MAX_VALUE - 8; //并发级别，遗留下来的，为兼容以前的版本 private static final int DEFAULT_CONCURRENCY_LEVEL = 16; // 负载因子 private static final float LOAD_FACTOR = 0.75f; // 链表转红黑树阀值,> 8 链表转换为红黑树 static final int TREEIFY_THRESHOLD = 8; //树转链表阀值，小于等于6（tranfer时，lc、hc=0两个计数器分别++记录原bin、新binTreeNode数量，<=UNTREEIFY_THRESHOLD 则untreeify(lo)） static final int UNTREEIFY_THRESHOLD = 6; static final int MIN_TREEIFY_CAPACITY = 64; private static final int MIN_TRANSFER_STRIDE = 16; private static final int RESIZE_STAMP_BITS = 16; // 2^15-1，help resize的最大线程数 private static final int MAX_RESIZERS = (1 << (32 - RESIZE_STAMP_BITS)) - 1; // 32-16=16，sizeCtl中记录size大小的偏移量 private static final int RESIZE_STAMP_SHIFT = 32 - RESIZE_STAMP_BITS; // forwarding nodes的hash值 static final int MOVED = -1; // hash for forwarding nodes // 树根节点的hash值 static final int TREEBIN = -2; // hash for roots of trees // ReservationNode的hash值 static final int RESERVED = -3; // hash for transient reservations static final int HASH_BITS = 0x7fffffff; // usable bits of normal node hash // 可用处理器数量 static final int NCPU = Runtime.getRuntime().availableProcessors(); // 存放node的数组 transient volatile Node<K,V>[] table; /** * 控制标识符，用来控制table的初始化和扩容的操作，不同的值有不同的含义 * 当为负数时：-1代表正在初始化，-N代表有N-1个线程正在 进行扩容 * 当为0时：代表当时的table还没有被初始化 * 当为正数时：表示初始化或者下一次进行扩容的大小 */ private transient volatile int sizeCtl;3.5.2.2 NodeNode是ConcurrentHashMap存储结构的基本单元，继承于HashMap中的Entry，用于存储数据。源码分析： /* ---------------- Nodes -------------- */ /** * Key-value entry. This class is never exported out as a * user-mutable Map.Entry (i.e., one supporting setValue; see * MapEntry below), but can be used for read-only traversals used * in bulk tasks. Subclasses of Node with a negative hash field * are special, and contain null keys and values (but are never * exported). Otherwise, keys and vals are never null. */ static class Node<K,V> implements Map.Entry<K,V> { final int hash; final K key; // val和next都会在扩容时发生变化，所以加上volatile来保持可见性和禁止重排序 volatile V val; volatile Node<K,V> next; Node(int hash, K key, V val, Node<K,V> next) { this.hash = hash; this.key = key; this.val = val; this.next = next; } public final K getKey() { return key; } public final V getValue() { return val; } public final int hashCode() { return key.hashCode() ^ val.hashCode(); } public final String toString() { return Helpers.mapEntryToString(key, val); } // 不允许更新value public final V setValue(V value) { throw new UnsupportedOperationException(); } public final boolean equals(Object o) { Object k, v, u; Map.Entry<?,?> e; return ((o instanceof Map.Entry) && (k = (e = (Map.Entry<?,?>)o).getKey()) != null && (v = e.getValue()) != null && (k == key || k.equals(key)) && (v == (u = val) || v.equals(u))); } /** * Virtualized support for map.get(); overridden in subclasses. */ // 用于map中的get（）方法，子类重写 Node<K,V> find(int h, Object k) { Node<K,V> e = this; if (k != null) { do { K ek; if (e.hash == h && ((ek = e.key) == k || (ek != null && k.equals(ek)))) return e; } while ((e = e.next) != null); } return null; } }Node数据结构很简单，从上可知，就是一个链表，但是只允许对数据进行查找，不允许进行修改。3.5.2.3 TreeNodeTreeNode继承与Node，但是数据结构换成了二叉树结构，它是红黑树的数据的存储结构，用于红黑树中存储数据，当链表的节点数大于8时会转换成红黑树的结构，他就是通过TreeNode作为存储结构代替Node来转换成黑红树。源码分析： /** * Nodes for use in TreeBins. */ static final class TreeNode<K,V> extends Node<K,V> { // 树形结构的属性定义 TreeNode<K,V> parent; // red-black tree links TreeNode<K,V> left; TreeNode<K,V> right; TreeNode<K,V> prev; // needed to unlink next upon deletion boolean red; // 标志红黑树的红节点 TreeNode(int hash, K key, V val, Node<K,V> next, TreeNode<K,V> parent) { super(hash, key, val, next); this.parent = parent; } Node<K,V> find(int h, Object k) { return findTreeNode(h, k, null); } /** * Returns the TreeNode (or null if not found) for the given key * starting at given root. */ // 根据key查找，从根节点开始找出相应的TreeNode。 final TreeNode<K,V> findTreeNode(int h, Object k, Class<?> kc) { if (k != null) { TreeNode<K,V> p = this; do { int ph, dir; K pk; TreeNode<K,V> q; TreeNode<K,V> pl = p.left, pr = p.right; if ((ph = p.hash) > h) p = pl; else if (ph < h) p = pr; else if ((pk = p.key) == k || (pk != null && k.equals(pk))) return p; else if (pl == null) p = pr; else if (pr == null) p = pl; else if ((kc != null || (kc = comparableClassFor(k)) != null) && (dir = compareComparables(kc, k, pk)) != 0) p = (dir < 0) ? pl : pr; else if ((q = pr.findTreeNode(h, k, kc)) != null) return q; else p = pl; } while (p != null); } return null; } }3.5.2.4 TreeBinTreeBin从字面含义中可以理解为存储树形结构的容器，而树形结构就是指TreeNode，所以TreeBin就是封装TreeNode的容器，它提供转换黑红树的一些条件和锁的控制。部分源码分析： /** * TreeNodes used at the heads of bins. TreeBins do not hold user * keys or values, but instead point to list of TreeNodes and * their root. They also maintain a parasitic read-write lock * forcing writers (who hold bin lock) to wait for readers (who do * not) to complete before tree restructuring operations. */ static final class TreeBin<K,V> extends Node<K,V> { // 指向TreeNode列表和根节点 TreeNode<K,V> root; volatile TreeNode<K,V> first; volatile Thread waiter; volatile int lockState; // values for lockState // 读写锁状态 static final int WRITER = 1; // set while holding write lock static final int WAITER = 2; // set when waiting for write lock static final int READER = 4; // increment value for setting read lock /** * Tie-breaking utility for ordering insertions when equal * hashCodes and non-comparable. We don't require a total * order, just a consistent insertion rule to maintain * equivalence across rebalancings. Tie-breaking further than * necessary simplifies testing a bit. */ static int tieBreakOrder(Object a, Object b) { int d; if (a == null || b == null || (d = a.getClass().getName(). compareTo(b.getClass().getName())) == 0) d = (System.identityHashCode(a) <= System.identityHashCode(b) ? -1 : 1); return d; } /** * Creates bin with initial set of nodes headed by b. * 初始化红黑树 */ TreeBin(TreeNode<K,V> b) { super(TREEBIN, null, null, null); this.first = b; TreeNode<K,V> r = null; for (TreeNode<K,V> x = b, next; x != null; x = next) { next = (TreeNode<K,V>)x.next; x.left = x.right = null; if (r == null) { x.parent = null; x.red = false; r = x; } else { K k = x.key; int h = x.hash; Class<?> kc = null; for (TreeNode<K,V> p = r;;) { int dir, ph; K pk = p.key; if ((ph = p.hash) > h) dir = -1; else if (ph < h) dir = 1; else if ((kc == null && (kc = comparableClassFor(k)) == null) || (dir = compareComparables(kc, k, pk)) == 0) dir = tieBreakOrder(k, pk); TreeNode<K,V> xp = p; if ((p = (dir <= 0) ? p.left : p.right) == null) { x.parent = xp; if (dir <= 0) xp.left = x; else xp.right = x; r = balanceInsertion(r, x); break; } } } } this.root = r; assert checkInvariants(root); } ... ... }构造函数就不多作解释，可以自行看源码理解。3.5.3 tableSizeFor方法tableSizeFor(int c)的原理：将c最高位以下通过|=运算全部变成1，最后返回的时候，返回n+1；eg:当输入为25的时候，n等于24，转成二进制为1100，右移1位为0110，将1100与0110进行或("|")操作，得到1110。接下来右移两位得11，再进行或操作得1111，接下来操作n的值就不会变化了。最后返回的时候，返回n+1，也就是10000，十进制为32。按照这种逻辑得到2的n次幂的数。那么为什么要先-1再+1呢？输入若是为0，那么不论怎么操作，n还是0，但是HashMap的容量只有大于0时才有意义。在ConcurrentHashMap实例中，设置初始大小会调整table大小，假设设置参数为100，最终会调整为256，确保table的大小总是2的幂次方，有人会问，为啥不是128，这里就要考虑到Load Factor，默认0.75，如果是128，那么128 * 0.75 = 96 < 100。源码分析： /** * Returns a power of two table size for the given desired capacity. * See Hackers Delight, sec 3.2 */ private static final int tableSizeFor(int c) { int n = c - 1; n |= n >>> 1; n |= n >>> 2; n |= n >>> 4; n |= n >>> 8; n |= n >>> 16; return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1; }注意，ConcurrentHashMap在构造函数中只会初始化sizeCtl值，并不会直接初始化table，而是延缓到第一次put操作。3.5.4 table初始化前面已经提到过，table初始化操作会延缓到第一次put行为。但是put是可以并发执行的，Doug Lea是如何实现table只初始化一次的？源码分析： /** * Initializes table, using the size recorded in sizeCtl. */ private final Node<K,V>[] initTable() { Node<K,V>[] tab; int sc; while ((tab = table) == null || tab.length == 0) { // 空的table才能进入初始化操作 // 如果一个线程发现sizeCtl<0，意味着另外的线程执行CAS操作成功，当前线程只需要让出cpu时间片 // 由于sizeCtl是volatile的，保证了顺序性和可见性 if ((sc = sizeCtl) < 0) // sc保存了sizeCtl的值， Thread.yield(); // lost initialization race; just spin else if (U.compareAndSwapInt(this, SIZECTL, sc, -1)) { // CAS操作SIZECTL为-1，表示初始化状态 try { if ((tab = table) == null || tab.length == 0) { // DEFAULT_CAPACITY = 16，若没有参数则大小默认为16 int n = (sc > 0) ? sc : DEFAULT_CAPACITY; @SuppressWarnings("unchecked") Node<K,V>[] nt = (Node<K,V>[])new Node<?,?>[n]; table = tab = nt; sc = n - (n >>> 2); // 记录下次扩容的大小 } } finally { sizeCtl = sc; } break; } } return tab; }sizeCtl默认为0，如果ConcurrentHashMap实例化时有传参数，sizeCtl会是一个2的幂次方的值。所以执行第一次put操作的线程会执行Unsafe.compareAndSwapInt方法修改sizeCtl为-1，有且只有一个线程能够修改成功，其它线程通过Thread.yield()让出CPU时间片等待table初始化完成。3.5.5 put方法put操作采用CAS+synchronized实现并发插入或更新操作。他在并发处理中使用的是乐观锁，当有冲突的时候才进行并发处理。源码分析： /** Implementation for put and putIfAbsent */ final V putVal(K key, V value, boolean onlyIfAbsent) { if (key == null || value == null) throw new NullPointerException(); int hash = spread(key.hashCode()); // 哈希算法 int binCount = 0; for (Node<K,V>[] tab = table;;) { // 无限循环，确保插入成功 Node<K,V> f; int n, i, fh; if (tab == null || (n = tab.length) == 0) // 表为空或表长度为0 tab = initTable(); // 初始化表 else if ((f = tabAt(tab, i = (n - 1) & hash)) == null) { // i = (n - 1) & hash为索引值，查找该元素 // 如果为null,说明第一次插入 if (casTabAt(tab, i, null, new Node<K,V>(hash, key, value, null))) break; // no lock when adding to empty bin } // MOVED=-1;当前正在扩容，一起进行扩容操作 else if ((fh = f.hash) == MOVED) tab = helpTransfer(tab, f); else { V oldVal = null; // 如果以上条件都不满足，那就要进行加锁操作，也就是存在hash冲突，锁住链表或者红黑树的头结点 synchronized (f) { if (tabAt(tab, i) == f) { if (fh >= 0) { // 表示该节点是链表结构 binCount = 1; for (Node<K,V> e = f;; ++binCount) { K ek; // 相同的key和hash进行put就会覆盖原先的value if (e.hash == hash && ((ek = e.key) == key || (ek != null && key.equals(ek)))) { oldVal = e.val; if (!onlyIfAbsent) e.val = value; break; } Node<K,V> pred = e; if ((e = e.next) == null) { // 插入链表尾部 pred.next = new Node<K,V>(hash, key, value, null); break; } } } else if (f instanceof TreeBin) { // 红黑树结构 Node<K,V> p; binCount = 2; // 红黑树结构旋转插入 if ((p = ((TreeBin<K,V>)f).putTreeVal(hash, key, value)) != null) { oldVal = p.val; if (!onlyIfAbsent) p.val = value; } } else if (f instanceof ReservationNode) throw new IllegalStateException("Recursive update"); } } if (binCount != 0) { // 如果链表的长度大于8时就会进行红黑树的转换 if (binCount >= TREEIFY_THRESHOLD) treeifyBin(tab, i); if (oldVal != null) return oldVal; break; } } } addCount(1L, binCount); //统计size，并且检查是否需要扩容 return null; } //哈希算法 static final int spread(int h) { return (h ^ (h >>> 16)) & HASH_BITS; } //保证拿到最新的数据 static final <K,V> Node<K,V> tabAt(Node<K,V>[] tab, int i) { return (Node<K,V>)U.getObjectAcquire(tab, ((long)i << ASHIFT) + ABASE); } //CAS操作插入节点，比较数组下标为i的节点是否为c，若是，用v交换，否则不操作。 //如果CAS成功，表示插入成功，结束循环进行addCount(1L, binCount)看是否需要扩容 static final <K,V> boolean casTabAt(Node<K,V>[] tab, int i, Node<K,V> c, Node<K,V> v) { return U.compareAndSetObject(tab, ((long)i << ASHIFT) + ABASE, c, v); } /** * Helps transfer if a resize is in progress. * 帮助从旧的table的元素复制到新的table中 */ final Node<K,V>[] helpTransfer(Node<K,V>[] tab, Node<K,V> f) { Node<K,V>[] nextTab; int sc; // 新的table nextTba已经存在前提下才能帮助扩容 if (tab != null && (f instanceof ForwardingNode) && (nextTab = ((ForwardingNode<K,V>)f).nextTable) != null) { int rs = resizeStamp(tab.length); while (nextTab == nextTable && table == tab && (sc = sizeCtl) < 0) { if ((sc >>> RESIZE_STAMP_SHIFT) != rs || sc == rs + 1 || sc == rs + MAX_RESIZERS || transferIndex <= 0) break; if (U.compareAndSwapInt(this, SIZECTL, sc, sc + 1)) { transfer(tab, nextTab); // 调用扩容方法 break; } } return nextTab; } return table; }table中定位索引位置，n是table的大小(n - 1) & hash获取table中对应索引的元素f。 Doug Lea采用Unsafe.getObjectVolatile来获取，也许有人质疑，直接table[index]不可以么，为什么要这么复杂？在java内存模型中，我们已经知道每个线程都有一个工作内存，里面存储着table的副本，虽然table是volatile修饰的，但不能保证线程每次都拿到table中的最新元素，Unsafe.getObjectVolatile可以直接获取指定内存的数据，保证了每次拿到数据都是最新的。如果f为null，说明table中这个位置第一次插入元素，没有hash冲突，利用Unsafe.compareAndSwapObject方法插入Node节点。如果CAS成功，说明Node节点已经插入，随后addCount(1L, binCount)方法会检查当前容量是否需要进行扩容。如果CAS失败，说明有其它线程提前插入了节点，自旋重新尝试在这个位置插入节点。如果f的hash值为-1，说明当前f是ForwardingNode节点，意味有其它线程正在扩容，则一起进行扩容操作。如果hash冲突，把新的Node节点按链表或红黑树的方式插入到合适的位置，这个过程采用同步内置锁实现并发。在节点f上进行同步，节点插入之前，再次利用tabAt(tab, i) == f判断，防止被其它线程修改。1. 如果f.hash >= 0，说明f是链表结构的头结点，遍历链表，如果找到对应的node节点，则修改value，否则在链表尾部加入节点。2. 如果f是TreeBin类型节点，说明f是红黑树根节点，则在树结构上遍历元素，更新或增加节点。3. 如果链表中节点数binCount >= TREEIFY_THRESHOLD(默认是8)，则把链表转化为红黑树结构。其中，helpTransfer（）方法的目的就是调用多个工作线程一起帮助进行扩容，这样的效率就会更高，而不是只有检查到要扩容的那个线程进行扩容操作，其他线程就要等待扩容操作完成才能工作。transfer()方法详情见3.5.5 table扩容。红黑树处理详见3.5.6 红黑树。3.5.5 table扩容当table容量不足的时候，即table的元素数量达到容量阈值sizeCtl，需要对table进行扩容。整个扩容分为两部分：1. 构建一个nextTable，大小为table的两倍。2. 把table的数据复制到nextTable中。扩容过程有点复杂，这里主要涉及到多线程并发扩容,ForwardingNode的作用就是支持扩容操作，将已处理的节点和空节点置为ForwardingNode，并发处理时多个线程经过ForwardingNode就表示已经遍历了，就往后遍历。多线程合作扩容的过程图：源码分析： /** * Adds to count, and if table is too small and not already * resizing, initiates transfer. If already resizing, helps * perform transfer if work is available. Rechecks occupancy * after a transfer to see if another resize is already needed * because resizings are lagging additions. * * @param x the count to add * @param check if <0, don't check resize, if <= 1 only check if uncontended */ private final void addCount(long x, int check) { CounterCell[] as; long b, s; // 更新baseCount，table的数量，counterCells表示元素个数的变化 if ((as = counterCells) != null || !U.compareAndSwapLong(this, BASECOUNT, b = baseCount, s = b + x)) { CounterCell a; long v; int m; boolean uncontended = true; // 如果多个线程都在执行，则CAS失败，执行fullAddCount，全部加入count if (as == null || (m = as.length - 1) < 0 || (a = as[ThreadLocalRandom.getProbe() & m]) == null || !(uncontended = U.compareAndSwapLong(a, CELLVALUE, v = a.value, v + x))) { fullAddCount(x, uncontended); return; } if (check <= 1) return; s = sumCount(); } // check>=0表示需要进行扩容操作 if (check >= 0) { Node<K,V>[] tab, nt; int n, sc; while (s >= (long)(sc = sizeCtl) && (tab = table) != null && (n = tab.length) < MAXIMUM_CAPACITY) { int rs = resizeStamp(n); if (sc < 0) { // sc < 0 表明此时有别的线程正在进行扩容 if ((sc >>> RESIZE_STAMP_SHIFT) != rs || sc == rs + 1 || sc == rs + MAX_RESIZERS || (nt = nextTable) == null || transferIndex <= 0) break; // 不满足前面5个条件时，尝试参与此次扩容 // 把正在执行transfer任务的线程数加1，+2代表有1个，+1代表有0个 if (U.compareAndSwapInt(this, SIZECTL, sc, sc + 1)) transfer(tab, nt); } // 试着让自己成为第一个执行transfer任务的线程 else if (U.compareAndSwapInt(this, SIZECTL, sc, (rs << RESIZE_STAMP_SHIFT) + 2)) transfer(tab, null); // 去执行transfer任务 s = sumCount(); // 重新计数，判断是否需要开启下一轮扩容 } } } /** * Moves and/or copies the nodes in each bin to new table. See * above for explanation. */ private final void transfer(Node<K,V>[] tab, Node<K,V>[] nextTab) { int n = tab.length, stride; // 每核处理的量小于16，则强制赋值16 if ((stride = (NCPU > 1) ? (n >>> 3) / NCPU : n) < MIN_TRANSFER_STRIDE) stride = MIN_TRANSFER_STRIDE; // subdivide range if (nextTab == null) { // initiating try { // 构建一个nextTable对象，其容量为原来容量的两倍 @SuppressWarnings("unchecked") Node<K,V>[] nt = (Node<K,V>[])new Node<?,?>[n << 1]; nextTab = nt; } catch (Throwable ex) { // try to cope with OOME sizeCtl = Integer.MAX_VALUE; return; } nextTable = nextTab; transferIndex = n; } int nextn = nextTab.length; // 连接点指针，用于标志位（fwd的hash值为-1，fwd.nextTable=nextTab） ForwardingNode<K,V> fwd = new ForwardingNode<K,V>(nextTab); // 当advance == true时，表明该节点已经处理过了 boolean advance = true; boolean finishing = false; // to ensure sweep before committing nextTab for (int i = 0, bound = 0;;) { Node<K,V> f; int fh; // 控制 --i ,遍历原hash表中的节点 while (advance) { int nextIndex, nextBound; if (--i >= bound || finishing) advance = false; else if ((nextIndex = transferIndex) <= 0) { i = -1; advance = false; } // 用CAS计算得到的transferIndex else if (U.compareAndSwapInt (this, TRANSFERINDEX, nextIndex, nextBound = (nextIndex > stride ? nextIndex - stride : 0))) { bound = nextBound; i = nextIndex - 1; advance = false; } } if (i < 0 || i >= n || i + n >= nextn) { int sc; // 已经完成所有节点复制了 if (finishing) { nextTable = null; table = nextTab; // table 指向nextTable sizeCtl = (n << 1) - (n >>> 1); // sizeCtl阈值为原来的1.5倍 return; // 跳出死循环 } // CAS 更扩容阈值，在这里面sizectl值减一，说明新加入一个线程参与到扩容操作 if (U.compareAndSwapInt(this, SIZECTL, sc = sizeCtl, sc - 1)) { if ((sc - 2) != resizeStamp(n) << RESIZE_STAMP_SHIFT) return; finishing = advance = true; i = n; // recheck before commit } } // 遍历的节点为null，则放入到ForwardingNode 指针节点 else if ((f = tabAt(tab, i)) == null) advance = casTabAt(tab, i, null, fwd); // f.hash == -1 表示遍历到了ForwardingNode节点，意味着该节点已经处理过了 // 这里是控制并发扩容的核心 else if ((fh = f.hash) == MOVED) advance = true; // already processed else { // 节点加锁 synchronized (f) { // 节点复制工作 if (tabAt(tab, i) == f) { Node<K,V> ln, hn; // fh >= 0 ,表示为链表节点 if (fh >= 0) { // 构造两个链表 一个是原链表 另一个是原链表的反序排列 int runBit = fh & n; Node<K,V> lastRun = f; for (Node<K,V> p = f.next; p != null; p = p.next) { int b = p.hash & n; if (b != runBit) { runBit = b; lastRun = p; } } if (runBit == 0) { ln = lastRun; hn = null; } else { hn = lastRun; ln = null; } for (Node<K,V> p = f; p != lastRun; p = p.next) { int ph = p.hash; K pk = p.key; V pv = p.val; if ((ph & n) == 0) ln = new Node<K,V>(ph, pk, pv, ln); else hn = new Node<K,V>(ph, pk, pv, hn); } // 在nextTable i 位置处插上链表 setTabAt(nextTab, i, ln); // 在nextTable i + n 位置处插上链表 setTabAt(nextTab, i + n, hn); // 在table i 位置处插上ForwardingNode 表示该节点已经处理过了 setTabAt(tab, i, fwd); // advance = true 可以执行--i动作，遍历节点 advance = true; } // 如果是TreeBin，则按照红黑树进行处理，处理逻辑与上面一致 else if (f instanceof TreeBin) { TreeBin<K,V> t = (TreeBin<K,V>)f; TreeNode<K,V> lo = null, loTail = null; TreeNode<K,V> hi = null, hiTail = null; int lc = 0, hc = 0; for (Node<K,V> e = t.first; e != null; e = e.next) { int h = e.hash; TreeNode<K,V> p = new TreeNode<K,V> (h, e.key, e.val, null, null); if ((h & n) == 0) { if ((p.prev = loTail) == null) lo = p; else loTail.next = p; loTail = p; ++lc; } else { if ((p.prev = hiTail) == null) hi = p; else hiTail.next = p; hiTail = p; ++hc; } } // 扩容后树节点个数若<=6，将树转链表 ln = (lc <= UNTREEIFY_THRESHOLD) ? untreeify(lo) : (hc != 0) ? new TreeBin<K,V>(lo) : t; hn = (hc <= UNTREEIFY_THRESHOLD) ? untreeify(hi) : (lc != 0) ? new TreeBin<K,V>(hi) : t; setTabAt(nextTab, i, ln); setTabAt(nextTab, i + n, hn); setTabAt(tab, i, fwd); advance = true; } } } } } }构建一个nextTable，这个过程只能只有单个线程进行nextTable的初始化。通过Unsafe.compareAndSwapInt修改sizeCtl值，保证只有一个线程能够初始化nextTable，扩容后的数组长度为原来的两倍，但是容量是原来的1.5。节点从table移动到nextTable，大体思想是遍历、复制的过程。1. 首先根据运算得到需要遍历的次数i，然后利用tabAt方法获得i位置的元素f，初始化一个forwardNode实例fwd。2. 如果f == null，则在table中的i位置放入fwd，这个过程是采用Unsafe.compareAndSwapObjectf方法实现的，很巧妙的实现了节点的并发移动。3. 如果f是链表的头节点，就构造一个反序链表，把他们分别放在nextTable的i和i+n的位置上，移动完成，采用Unsafe.putObjectVolatile方法给table原位置赋值fwd。4. 如果f是TreeBin节点，也做一个反序处理，并判断是否需要untreeify，把处理的结果分别放在nextTable的i和i+n的位置上，移动完成，同样采用Unsafe.putObjectVolatile方法给table原位置赋值fwd。遍历过所有的节点以后就完成了复制工作，把table指向nextTable，并更新sizeCtl为新数组大小的0.75倍，扩容完成。3.5.6 红黑树这个后面专门写一篇文章对红黑树源码分析，这里可以先看看在ConcurrentHashMap中红黑树的使用。主要是treeifyBin(Node<K,V>[] tab, int index)方法，作用是链表转红黑树。源码分析： /** * Replaces all linked nodes in bin at given index unless table is * too small, in which case resizes instead. */ private final void treeifyBin(Node<K,V>[] tab, int index) { Node<K,V> b; int n; if (tab != null) { // 如果整个table的数量小于64，就扩容至原来的一倍，不转红黑树了 // 因为这个阈值扩容可以减少hash冲突，不必要去转红黑树 if ((n = tab.length) < MIN_TREEIFY_CAPACITY) tryPresize(n << 1); else if ((b = tabAt(tab, index)) != null && b.hash >= 0) { synchronized (b) { if (tabAt(tab, index) == b) { TreeNode<K,V> hd = null, tl = null; for (Node<K,V> e = b; e != null; e = e.next) { // 封装成TreeNode TreeNode<K,V> p = new TreeNode<K,V>(e.hash, e.key, e.val, null, null); if ((p.prev = tl) == null) hd = p; else tl.next = p; tl = p; } // 通过TreeBin对象对TreeNode转换成红黑树 setTabAt(tab, index, new TreeBin<K,V>(hd)); } } } } }可以看出，生成树节点的代码块是同步的，进入同步代码块之后，再次验证table中index位置元素是否被修改过。1. 根据table中index位置Node链表，重新生成一个hd为头结点的TreeNode链表。2. 根据hd头结点，生成TreeBin树结构，并把树结构的root节点写到table的index位置的内存中。TreenBin详见前面 3.5.2.4 TreenBin。3.5.7 get方法get操作相对于put简单一些。判断table是否为空，如果为空，直接返回null。计算key的hash值，并获取指定table中指定位置的Node节点，通过遍历链表或则树结构找到对应的节点，返回value值。如果遇到扩容的时候，会调用标志正在扩容节点ForwardingNode的find方法，查找该节点，匹配就返回源码分析： /** * Returns the value to which the specified key is mapped, * or {@code null} if this map contains no mapping for the key. * * <p>More formally, if this map contains a mapping from a key * {@code k} to a value {@code v} such that {@code key.equals(k)}, * then this method returns {@code v}; otherwise it returns * {@code null}. (There can be at most one such mapping.) * * @throws NullPointerException if the specified key is null */ public V get(Object key) { Node<K,V>[] tab; Node<K,V> e, p; int n, eh; K ek; int h = spread(key.hashCode()); // hash计算 if ((tab = table) != null && (n = tab.length) > 0 && (e = tabAt(tab, (n - 1) & h)) != null) { // 读取首节点的Node元素 if ((eh = e.hash) == h) { // 如果该节点就是首节点就返回 if ((ek = e.key) == key || (ek != null && key.equals(ek))) return e.val; } // hash值为负值表示正在扩容 // 这个时候查的是ForwardingNode的find方法来定位到nextTable来查找，查找到就返回 else if (eh < 0) return (p = e.find(h, key)) != null ? p.val : null; while ((e = e.next) != null) { //既不是首节点也不是ForwardingNode，那就往下遍历 if (e.hash == h && ((ek = e.key) == key || (ek != null && key.equals(ek)))) return e.val; } } return null; }3.5.8 size方法在JDK1.8版本中，对于size的计算，在扩容和addCount()方法就已经有处理了，JDK1.7（源码需要自己看，就不讲解了）是在调用size()方法才去计算，其实在并发集合中去计算size是没有多大的意义的，因为size是实时在变的，只能计算某一刻的大小，但是某一刻太快了，人的感知是一个时间段，所以并不是很精确。源码分析： /** * {@inheritDoc} JDK1.8 */ public int size() { long n = sumCount(); return ((n < 0L) ? 0 : (n > (long)Integer.MAX_VALUE) ? Integer.MAX_VALUE : (int)n); }3.5.9 ConcurrentHashMap总结Hashtable的任何操作都会把整个表锁住，是阻塞的。好处是总能获取最实时的更新，比如说线程A调用putAll写入大量数据，期间线程B调用get，线程B就会被阻塞，直到线程A完成putAll，因此线程B肯定能获取到线程A写入的完整数据。坏处是所有调用都要排队，效率较低。ConcurrentHashMap 是设计为非阻塞的。在更新时会局部锁住某部分数据，但不会把整个表都锁住。同步读取操作则是完全非阻塞的。好处是在保证合理的同步前提下，效率很高。坏处是严格来说读取操作不能保证反映最近的更新。例如线程A调用putAll写入大量数据，期间线程B调用get，则只能get到目前为止已经顺利插入的部分数据。应该根据具体的应用场景选择合适的HashMap。其实可以看出JDK1.8版本的ConcurrentHashMap的数据结构已经接近HashMap，相对而言，ConcurrentHashMap只是增加了同步的操作来控制并发，从JDK1.7版本的ReentrantLock+Segment+HashEntry，到JDK1.8版本中synchronized+CAS+HashEntry+红黑树,相对而言，总结如下思考：1. JDK1.8的实现降低锁的粒度，JDK1.7版本锁的粒度是基于Segment的，包含多个HashEntry，而JDK1.8锁的粒度就是HashEntry（首节点）。2. JDK1.8版本的数据结构变得更加简单，使得操作也更加清晰流畅，因为已经使用synchronized来进行同步，所以不需要分段锁的概念，也就不需要Segment这种数据结构了，由于粒度的降低，实现的复杂度也增加了。3. JDK1.8使用红黑树来优化链表，基于长度很长的链表的遍历是一个很漫长的过程，而红黑树的遍历效率是很快的，代替一定阈值的链表，这样形成一个最佳拍档。4. JDK1.8为什么使用内置锁synchronized来代替重入锁ReentrantLock，有以下几点：1. 因为粒度降低了，在相对而言的低粒度加锁方式，synchronized并不比ReentrantLock差，在粗粒度加锁中ReentrantLock可能通过Condition来控制各个低粒度的边界，更加的灵活，而在低粒度中，Condition的优势就没有了。2. JVM的开发团队从来都没有放弃synchronized，而且基于JVM的synchronized优化空间更大，使用内嵌的关键字比使用API更加自然。3. 在大量的数据操作下，对于JVM的内存压力，基于API的ReentrantLock会开销更多的内存，虽然不是瓶颈，但是也是一个选择依据。3.6 LinkedHashMap3.6.1 概括通过上面 3.4 HashMap 可以了解到HashMap是无序的，而有序的则是LinkedHashMap，虽然增加了时间和空间上的开销，但是LinkedHashMap保证所有了元素迭代的顺序，它维护着一个运行于所有条目的双重链接列表。LinkedHashMap是继承HashMap，底层基于拉链式散列结构，使用哈希表与双向链表来保存所有元素（数组和链表或红黑树组成），key-valu都允许为空，同样，它也是不同步的，也就是线程不安全。它的基本思想就是多态，它使用LinkedList维护插入元素的先后顺序。下面是LinkedHashMap与HashMap结构上的对比可以看出，相比较HashMap，在其基础上增加了一条双向链表，使得上面的结构可以保持键值对的插入顺序。同时通过对链表进行相应的操作，实现了访问顺序相关逻辑。每当有新键值对节点插入，新节点最终会接在 tail 引用指向的节点后面。而 tail 引用则会移动到新的节点上，这样一个双向链表就建立起来了。header是一个空节点，该节点不存放key-value内容，为LinkedHashMap类的成员属性，循环双向链表的入口。初始化后header结构：其中，它的hash值为-1，其他都为null，也就是说这个header不存放在数组中，就是用来指示开始元素和结束元素的。header的目的是为了记录第一个插入的元素是谁，在遍历的时候能够找到第一个元素。3.6.2 成员变量private static final long serialVersionUID = 3801124242820219131L; // 用于指向双向链表的头部 transient LinkedHashMap.Entry<K,V> head; //用于指向双向链表的尾部 transient LinkedHashMap.Entry<K,V> tail; /** * 用来指定LinkedHashMap的迭代顺序， * true则表示按照基于访问的顺序来排列，意思就是最近使用的entry，放在链表的最末尾 * false则表示按照插入顺序来 */ final boolean accessOrder;注意：accessOrder的final关键字，说明我们要在构造方法里给它初始化。3.6.3 构造方法下面是空参构造方法源码： /** * Constructs an empty insertion-ordered <tt>LinkedHashMap</tt> instance * with the default initial capacity (16) and load factor (0.75). */ public LinkedHashMap() { // 调用HashMap的构造方法 super(); // 这里是指是否基于访问排序，默认为false accessOrder = false; }这里讲解讲解一下accessOrder这个布尔值，LinkedHashMap存储是有序的，分两种：1. 插入顺序 2. 访问顺序。而在空参构造函数中accessOrder = false，这就表示顺序是以插入插入顺序，而不是访问顺序，也就是说LinkedHashMap中存储的顺序是按照调用put方法插入的顺序进行排序的。当accessOrder = true时，调用get方法就会使获取数据对应的Entry（Android中LinkedHashMapEntry）移动到最后。LinkedHashMap也提供了设置accessOrder的构造方法，下面是构造方法的源码： /** * Constructs an empty <tt>LinkedHashMap</tt> instance with the * specified initial capacity, load factor and ordering mode. * * @param initialCapacity the initial capacity * @param loadFactor the load factor * @param accessOrder the ordering mode - <tt>true</tt> for * access-order, <tt>false</tt> for insertion-order * @throws IllegalArgumentException if the initial capacity is negative * or the load factor is nonpositive */ public LinkedHashMap(int initialCapacity, float loadFactor, boolean accessOrder) { super(initialCapacity, loadFactor); // 设置accessOrder this.accessOrder = accessOrder; }其他的构造方法就不一一讲述了。3.6.4 Entry（Android中LinkedHashMapEntry）Entry（Android中LinkedHashMapEntry）是LinkedHashMap的内部类，继承父类是HashMap.Node<K,V>(JDK1.8，JDK1.7是HashMap.Entry<K,V>)，多了before和after两个引用，用于实现双向链表。源码分析：/** * HashMap.Node subclass for normal LinkedHashMap entries. * Android-》LinkedHashMapEntry Java-》Entry */ static class Entry<K,V> extends HashMap.Node<K,V> { Entry<K,V> before, after; Entry(int hash, K key, V value, Node<K,V> next) { super(hash, key, value, next); } } 3.6.5 put方法在LinkedHashMap中，它并没有覆写父类的put方法，但是在HashMap中，put方法插入的是HashMap中的内部类Node类型的节点，该类型的节点并不具备与LinkedHashMap内部类Entry（Android中LinkedHashMapEntry）及其子类型节点组成链表的能力，那么LinkedHashMap的链表如果建成的，下面先一起看看put方法的实现。// HashMap 中实现，详细的请看前面HashMap的讲解 final V putVal(int hash, K key, V value, boolean onlyIfAbsent, boolean evict) { Node<K,V>[] tab; Node<K,V> p; int n, i; if ((tab = table) == null || (n = tab.length) == 0) {...} // 通过节点 hash 定位节点所在的桶位置，并检测桶中是否包含节点引用 if ((p = tab[i = (n - 1) & hash]) == null) {...} else { Node<K,V> e; K k; if (p.hash == hash && ((k = p.key) == key || (key != null && key.equals(k)))) e = p; else if (p instanceof TreeNode) {...} else { // 遍历链表，并统计链表长度 for (int binCount = 0; ; ++binCount) { // 未在单链表中找到要插入的节点，将新节点接在单链表的后面 if ((e = p.next) == null) { p.next = newNode(hash, key, value, null); if (binCount >= TREEIFY_THRESHOLD - 1) {...} break; } // 插入的节点已经存在于单链表中 if (e.hash == hash && ((k = e.key) == key || (key != null && key.equals(k)))) break; p = e; } } if (e != null) { // existing mapping for key V oldValue = e.value; if (!onlyIfAbsent || oldValue == null) {...} afterNodeAccess(e); // 在节点被访问后移动链尾 return oldValue; } } ++modCount; if (++size > threshold) {...} afterNodeInsertion(evict); // 当插入时，将双向链表的头结点移除 return null; } // HashMap 中实现 Node<K,V> newNode(int hash, K key, V value, Node<K,V> next) { return new Node<>(hash, key, value, next); } // LinkedHashMap 中覆写 Node<K,V> newNode(int hash, K key, V value, Node<K,V> e) { LinkedHashMap.Entry<K,V> p = new LinkedHashMap.Entry<K,V>(hash, key, value, e); // 将 Entry 接在双向链表的尾部 linkNodeLast(p); return p; } // LinkedHashMap 中实现 private void linkNodeLast(LinkedHashMap.Entry<K,V> p) { // 将tail给临时变量last LinkedHashMap.Entry<K,V> last = tail; // 把new的Entry给tail tail = p; // last 为 null，表明链表还未建立，则p即为头结点也为尾节点 if (last == null) head = p; else { // 将新节点 p 接在链表尾部，after指针指向p，p的before指向之前链尾 p.before = last; last.after = p; } } // putTreeVal里有调用了这个 TreeNode<K,V> newTreeNode(int hash, K key, V value, Node<K,V> next) { TreeNode<K,V> p = new TreeNode<K,V>(hash, key, value, next); linkNodeLast(p); return p; } // LinkedHashMap 中实现 --- 在节点被访问后移动链尾 void afterNodeAccess(Node<K,V> e) { // move node to last LinkedHashMap.Entry<K,V> last; // 如果定义了accessOrder，那么就保证最近访问节点放到最后 if (accessOrder && (last = tail) != e) { LinkedHashMap.Entry<K,V> p = (LinkedHashMap.Entry<K,V>)e, b = p.before, a = p.after; // 因为要移动到链尾，所以先至尾指针为空 p.after = null; // 如果前面没有元素，则p之前为头结点，直接让a成为头结点 if (b == null) head = a; else // 否则b的尾指针指向a b.after = a; if (a != null) // 如果a不为空，则a的头指针指向b a.before = b; else /* * 这里存疑，父条件分支已经确保节点 e 不会是尾节点， * 那么 e.after 必然不会为 null，不知道 else 分支有什么作用 */ // 否则 p之前就为尾指针，则另b成为尾指针 last = b; if (last == null) // 如果双向链表中只有p一个节点，则令p即为头结点，也为尾节点 head = p; else { // 否则 将p插入链尾 p.before = last; last.after = p; } // 将p设置为将p设置为尾节点 tail = p; // 修改计数器+1 ++modCount; } } // LinkedHashMap 中实现 --- 当插入时，将双向链表的头结点移除 // LRU算法 void afterNodeInsertion(boolean evict) { // possibly remove eldest LinkedHashMap.Entry<K,V> first; // 根据条件判断是否移除最近最少被访问的节点（如果定义了溢出规则，则执行相应的溢出） if (evict && (first = head) != null && removeEldestEntry(first)) { K key = first.key; removeNode(hash(key), key, null, false, true); } } // 移除最近最少被访问条件之一，通过重写此方法可实现不同策略的缓存 protected boolean removeEldestEntry(Map.Entry<K,V> eldest) { return false; }从上面的源码可以看出，LinkedHashMap重写了newNode(int hash, K key, V value, Node<K,V> e)方法，在这个方法中，LinkedHashMap创建了Entry（Android中LinkedHashMapEntry），并通过linkNodeLast(LinkedHashMap.Entry<K,V> p)方法将Entry接在双向链表的尾部，实现了双向链表的建立。这里详解讲解一下afterNodeAccess方法：正常情况下：查询的p在链表中间，那么将p设置到末尾后，它原先的前节点b和后节点a就变成了前后节点。情况一：p为头部，前一个节点b不存在，那么考虑到p要放到最后面，则设置p的后一个节点a为head情况二：p为尾部，后一个节点a不存在，那么考虑到统一操作，设置last为b情况三：p为链表里的第一个节点，head=p图解：例子：对下图键值为3的节点访问，访问前后结构对比图：访问前：访问后：从上面对比可以看出，键值为3的节点将会被移动到双向链表的最后位置，其前驱和后继也会跟着更新。注意：这里只是指向改变了，实际上，桶的位置是没有变化的。3.6.6 get方法get方法主要看LinkedHashMap对访问顺序的维护，通过AccessOrder控制是否使用访问顺序。// LinkedHashMap 中覆写 public V get(Object key) { Node<K,V> e; // 这里不懂就回HashMap看看 if ((e = getNode(hash(key), key)) == null) return null; // 如果 accessOrder 为 true，则调用 afterNodeAccess 将被访问节点移动到链表最后 if (accessOrder) afterNodeAccess(e); return e.value; } 其中afterNodeAccess方法在3.6.5 put方法 中源码已经详细分析过了，不懂的可以结合前面的看。3.6.7 remove方法remove方法和put方法一样，都是使用HashMap中的方法，在remove方法调用了removeNode方法，对于removeNode方法不熟悉的可以看上面HashMap中remove方法的讲解，在removeNode方法中有调用afterNodeRemoval方法，HashMap没有实现afterNodeRemoval方法，在LinkedHashMap中实现了，下面看看源码分析。源码分析：// e即是要删除的节点 void afterNodeRemoval(Node<K,V> e) { // unlink // 与afterNodeAccess方法一样，记录e的前后节点b，a LinkedHashMap.Entry<K,V> p = (LinkedHashMap.Entry<K,V>)e, b = p.before, a = p.after; // p已删除，前后指针都设置为null，便于GC回收 p.before = p.after = null; // 与afterNodeAccess方法一样类似，一顿判断，然后b，a互为前后节点 if (b == null) head = a; else b.after = a; if (a == null) tail = b; else a.before = b; }这个函数是在移除节点后调用的，就是将节点从双向链表中删除。3.6.8 LinkedHashMap迭代器看看就能懂...// Iterators abstract class LinkedHashIterator { // 记录下一个Entry LinkedHashMap.Entry<K, V> next; // 记录当前的Entry LinkedHashMap.Entry<K, V> current; // 记录是否发生了迭代过程中的修改 int expectedModCount; LinkedHashIterator() { // 初始化的时候把head给next next = head; expectedModCount = modCount; current = null; } public final boolean hasNext() { return next != null; } // 这里采用的是链表方式的遍历方式 final LinkedHashMap.Entry<K, V> nextNode() { LinkedHashMap.Entry<K, V> e = next; if (modCount != expectedModCount) throw new ConcurrentModificationException(); if (e == null) throw new NoSuchElementException(); // 记录当前的Entry current = e; // 直接拿after给next next = e.after; return e; } public final void remove() { Node<K, V> p = current; if (p == null) throw new IllegalStateException(); if (modCount != expectedModCount) throw new ConcurrentModificationException(); current = null; K key = p.key; removeNode(hash(key), key, null, false, false); expectedModCount = modCount; } } final class LinkedKeyIterator extends LinkedHashIterator implements Iterator<K> { public final K next() { return nextNode().getKey(); } } final class LinkedValueIterator extends LinkedHashIterator implements Iterator<V> { public final V next() { return nextNode().value; } } final class LinkedEntryIterator extends LinkedHashIterator implements Iterator<Map.Entry<K,V>> { public final Map.Entry<K,V> next() { return nextNode(); } }3.6.9 总结1. LinkedHashMap继承于HashMap。2. LinkedHashMap中使用的LRU缓存策略算法，通过一些条件，判断是否移除最近被访问最少的节点。可以重写removeEldestEntry方法。3. 多的不说，总体来说，上面都有。3.7 TreeMap3.7.1 概括TreeMap最早出现在JDK1.2版本，它底层是基于红黑树实现的，时间复杂度log(n)。TreeMap的key按照自然顺序进行排列或根据创建时提供的comparator接口进行排序，从存储角度来讲，与HashMap的O(1)时间复杂度差一些，但是在统计功能上，TreeMap同样保证时间开销是log(n)，要优于HashMap的O(n)。TreeMapkey不允许为null，value允许为null，同时，它非同步，也就是线程不安全。如果我们希望Map可以保持key的大小顺序的时候，我们就需要利用TreeMap。总的来说，TreeMap很多方法是对红黑树中增删改查基础操作的一中包装。所以在学习TreeMap前建议先看看红黑树，不懂红黑树看你会很累的。后面文章会有补充。3.7.2 继承关系相比较HashMap，可以看出它实现了NavigableMap接口，在NavigableMap继承自SortedMap，这是一个排序接口，这也就TreeMap能够实现排序的原因。3.7.3 SortedMap接口SortedMap主要是Comparator接口，说到这个就要说说Comparable这个接口，这两个都差不多，Comparable自带比较功能，而Comparator是赋予没有比较能力的对象一种比较能力，例如：面对一道计算题，小明天生口算能力很强，看一眼就能算出来答案。而小李没有这种能力，需要借助计算器才能得出答案。先看看SortedMap接口的源码：public interface SortedMap<K,V> extends Map<K,V> { /** * Returns the comparator used to order the keys in this map, or * {@code null} if this map uses the {@linkplain Comparable * natural ordering} of its keys. * * @return the comparator used to order the keys in this map, * or {@code null} if this map uses the natural ordering * of its keys */ // 返回用于对键的进行排序的比较器，如果此映射使用其键的自然排序，则为null Comparator<? super K> comparator(); /** * Returns a view of the portion of this map whose keys range from * {@code fromKey}, inclusive, to {@code toKey}, exclusive. (If * {@code fromKey} and {@code toKey} are equal, the returned map * is empty.) The returned map is backed by this map, so changes * in the returned map are reflected in this map, and vice-versa. * The returned map supports all optional map operations that this * map supports. * * <p>The returned map will throw an {@code IllegalArgumentException} * on an attempt to insert a key outside its range. * * @param fromKey low endpoint (inclusive) of the keys in the returned map * @param toKey high endpoint (exclusive) of the keys in the returned map * @return a view of the portion of this map whose keys range from * {@code fromKey}, inclusive, to {@code toKey}, exclusive * @throws ClassCastException if {@code fromKey} and {@code toKey} * cannot be compared to one another using this map's comparator * (or, if the map has no comparator, using natural ordering). * Implementations may, but are not required to, throw this * exception if {@code fromKey} or {@code toKey} * cannot be compared to keys currently in the map. * @throws NullPointerException if {@code fromKey} or {@code toKey} * is null and this map does not permit null keys * @throws IllegalArgumentException if {@code fromKey} is greater than * {@code toKey}; or if this map itself has a restricted * range, and {@code fromKey} or {@code toKey} lies * outside the bounds of the range */ // 返回从fromKey（包括）到toKey（不包括）之间的map SortedMap<K,V> subMap(K fromKey, K toKey); /** * Returns a view of the portion of this map whose keys are * strictly less than {@code toKey}. The returned map is backed * by this map, so changes in the returned map are reflected in * this map, and vice-versa. The returned map supports all * optional map operations that this map supports. * * <p>The returned map will throw an {@code IllegalArgumentException} * on an attempt to insert a key outside its range. * * @param toKey high endpoint (exclusive) of the keys in the returned map * @return a view of the portion of this map whose keys are strictly * less than {@code toKey} * @throws ClassCastException if {@code toKey} is not compatible * with this map's comparator (or, if the map has no comparator, * if {@code toKey} does not implement {@link Comparable}). * Implementations may, but are not required to, throw this * exception if {@code toKey} cannot be compared to keys * currently in the map. * @throws NullPointerException if {@code toKey} is null and * this map does not permit null keys * @throws IllegalArgumentException if this map itself has a * restricted range, and {@code toKey} lies outside the * bounds of the range */ // 返回小于toKey的map SortedMap<K,V> headMap(K toKey); /** * Returns a view of the portion of this map whose keys are * greater than or equal to {@code fromKey}. The returned map is * backed by this map, so changes in the returned map are * reflected in this map, and vice-versa. The returned map * supports all optional map operations that this map supports. * * <p>The returned map will throw an {@code IllegalArgumentException} * on an attempt to insert a key outside its range. * * @param fromKey low endpoint (inclusive) of the keys in the returned map * @return a view of the portion of this map whose keys are greater * than or equal to {@code fromKey} * @throws ClassCastException if {@code fromKey} is not compatible * with this map's comparator (or, if the map has no comparator, * if {@code fromKey} does not implement {@link Comparable}). * Implementations may, but are not required to, throw this * exception if {@code fromKey} cannot be compared to keys * currently in the map. * @throws NullPointerException if {@code fromKey} is null and * this map does not permit null keys * @throws IllegalArgumentException if this map itself has a * restricted range, and {@code fromKey} lies outside the * bounds of the range */ // 返回大于或等于fromKey的map SortedMap<K,V> tailMap(K fromKey); /** * Returns the first (lowest) key currently in this map. * * @return the first (lowest) key currently in this map * @throws NoSuchElementException if this map is empty */ // 返回map中第一个（最低）键 K firstKey(); /** * Returns the last (highest) key currently in this map. * * @return the last (highest) key currently in this map * @throws NoSuchElementException if this map is empty */ // 返回map中最后一个（最高）键 K lastKey(); /** * Returns a {@link Set} view of the keys contained in this map. * The set's iterator returns the keys in ascending order. * The set is backed by the map, so changes to the map are * reflected in the set, and vice-versa. If the map is modified * while an iteration over the set is in progress (except through * the iterator's own {@code remove} operation), the results of * the iteration are undefined. The set supports element removal, * which removes the corresponding mapping from the map, via the * {@code Iterator.remove}, {@code Set.remove}, * {@code removeAll}, {@code retainAll}, and {@code clear} * operations. It does not support the {@code add} or {@code addAll} * operations. * * @return a set view of the keys contained in this map, sorted in * ascending order */ Set<K> keySet(); /** * Returns a {@link Collection} view of the values contained in this map. * The collection's iterator returns the values in ascending order * of the corresponding keys. * The collection is backed by the map, so changes to the map are * reflected in the collection, and vice-versa. If the map is * modified while an iteration over the collection is in progress * (except through the iterator's own {@code remove} operation), * the results of the iteration are undefined. The collection * supports element removal, which removes the corresponding * mapping from the map, via the {@code Iterator.remove}, * {@code Collection.remove}, {@code removeAll}, * {@code retainAll} and {@code clear} operations. It does not * support the {@code add} or {@code addAll} operations. * * @return a collection view of the values contained in this map, * sorted in ascending key order */ Collection<V> values(); /** * Returns a {@link Set} view of the mappings contained in this map. * The set's iterator returns the entries in ascending key order. * The set is backed by the map, so changes to the map are * reflected in the set, and vice-versa. If the map is modified * while an iteration over the set is in progress (except through * the iterator's own {@code remove} operation, or through the * {@code setValue} operation on a map entry returned by the * iterator) the results of the iteration are undefined. The set * supports element removal, which removes the corresponding * mapping from the map, via the {@code Iterator.remove}, * {@code Set.remove}, {@code removeAll}, {@code retainAll} and * {@code clear} operations. It does not support the * {@code add} or {@code addAll} operations. * * @return a set view of the mappings contained in this map, * sorted in ascending key order */ Set<Map.Entry<K, V>> entrySet(); }Comparator接口讲解：这里先看看Comparable接口源码：public interface Comparable<T> { /** * Compares this object with the specified object for order. Returns a * negative integer, zero, or a positive integer as this object is less * than, equal to, or greater than the specified object. * * <p>The implementor must ensure <tt>sgn(x.compareTo(y)) == * -sgn(y.compareTo(x))</tt> for all <tt>x</tt> and <tt>y</tt>. (This * implies that <tt>x.compareTo(y)</tt> must throw an exception iff * <tt>y.compareTo(x)</tt> throws an exception.) * * <p>The implementor must also ensure that the relation is transitive: * <tt>(x.compareTo(y)&gt;0 &amp;&amp; y.compareTo(z)&gt;0)</tt> implies * <tt>x.compareTo(z)&gt;0</tt>. * * <p>Finally, the implementor must ensure that <tt>x.compareTo(y)==0</tt> * implies that <tt>sgn(x.compareTo(z)) == sgn(y.compareTo(z))</tt>, for * all <tt>z</tt>. * * <p>It is strongly recommended, but <i>not</i> strictly required that * <tt>(x.compareTo(y)==0) == (x.equals(y))</tt>. Generally speaking, any * class that implements the <tt>Comparable</tt> interface and violates * this condition should clearly indicate this fact. The recommended * language is "Note: this class has a natural ordering that is * inconsistent with equals." * * <p>In the foregoing description, the notation * <tt>sgn(</tt><i>expression</i><tt>)</tt> designates the mathematical * <i>signum</i> function, which is defined to return one of <tt>-1</tt>, * <tt>0</tt>, or <tt>1</tt> according to whether the value of * <i>expression</i> is negative, zero or positive. * * @param o the object to be compared. * @return a negative integer, zero, or a positive integer as this object * is less than, equal to, or greater than the specified object. * * @throws NullPointerException if the specified object is null * @throws ClassCastException if the specified object's type prevents it * from being compared to this object. */ // 如果小于o，返回负数；等于o，返回0；大于o返回正数。 public int compareTo(T o); }上面compareTo方法就是传入一个泛型T的对象o，对o进行比较，如果小于o，返回负数；等于o，返回0；大于o，返回正数。在看看Comparator接口的源码：@FunctionalInterface public interface Comparator<T> { /** * Compares its two arguments for order. Returns a negative integer, * zero, or a positive integer as the first argument is less than, equal * to, or greater than the second.<p> * * In the foregoing description, the notation * <tt>sgn(</tt><i>expression</i><tt>)</tt> designates the mathematical * <i>signum</i> function, which is defined to return one of <tt>-1</tt>, * <tt>0</tt>, or <tt>1</tt> according to whether the value of * <i>expression</i> is negative, zero or positive.<p> * * The implementor must ensure that <tt>sgn(compare(x, y)) == * -sgn(compare(y, x))</tt> for all <tt>x</tt> and <tt>y</tt>. (This * implies that <tt>compare(x, y)</tt> must throw an exception if and only * if <tt>compare(y, x)</tt> throws an exception.)<p> * * The implementor must also ensure that the relation is transitive: * <tt>((compare(x, y)&gt;0) &amp;&amp; (compare(y, z)&gt;0))</tt> implies * <tt>compare(x, z)&gt;0</tt>.<p> * * Finally, the implementor must ensure that <tt>compare(x, y)==0</tt> * implies that <tt>sgn(compare(x, z))==sgn(compare(y, z))</tt> for all * <tt>z</tt>.<p> * * It is generally the case, but <i>not</i> strictly required that * <tt>(compare(x, y)==0) == (x.equals(y))</tt>. Generally speaking, * any comparator that violates this condition should clearly indicate * this fact. The recommended language is "Note: this comparator * imposes orderings that are inconsistent with equals." * * @param o1 the first object to be compared. * @param o2 the second object to be compared. * @return a negative integer, zero, or a positive integer as the * first argument is less than, equal to, or greater than the * second. * @throws NullPointerException if an argument is null and this * comparator does not permit null arguments * @throws ClassCastException if the arguments' types prevent them from * being compared by this comparator. */ // 核心方法，用来比较两个对象，如果o1小于o2，返回负数；等于o2，返回0；大于o2返回正数 int compare(T o1, T o2); /** * Indicates whether some other object is &quot;equal to&quot; this * comparator. This method must obey the general contract of * {@link Object#equals(Object)}. Additionally, this method can return * <tt>true</tt> <i>only</i> if the specified object is also a comparator * and it imposes the same ordering as this comparator. Thus, * <code>comp1.equals(comp2)</code> implies that <tt>sgn(comp1.compare(o1, * o2))==sgn(comp2.compare(o1, o2))</tt> for every object reference * <tt>o1</tt> and <tt>o2</tt>.<p> * * Note that it is <i>always</i> safe <i>not</i> to override * <tt>Object.equals(Object)</tt>. However, overriding this method may, * in some cases, improve performance by allowing programs to determine * that two distinct comparators impose the same order. * * @param obj the reference object with which to compare. * @return <code>true</code> only if the specified object is also * a comparator and it imposes the same ordering as this * comparator. * @see Object#equals(Object) * @see Object#hashCode() */ boolean equals(Object obj); /** * Returns a comparator that imposes the reverse ordering of this * comparator. * * @return a comparator that imposes the reverse ordering of this * comparator. * @since 1.8 */ // 返回反向排序比 default Comparator<T> reversed() { return Collections.reverseOrder(this); } /** * Returns a lexicographic-order comparator with another comparator. * If this {@code Comparator} considers two elements equal, i.e. * {@code compare(a, b) == 0}, {@code other} is used to determine the order. * * <p>The returned comparator is serializable if the specified comparator * is also serializable. * * @apiNote * For example, to sort a collection of {@code String} based on the length * and then case-insensitive natural ordering, the comparator can be * composed using following code, * * <pre>{@code * Comparator<String> cmp = Comparator.comparingInt(String::length) * .thenComparing(String.CASE_INSENSITIVE_ORDER); * }</pre> * * @param other the other comparator to be used when this comparator * compares two objects that are equal. * @return a lexicographic-order comparator composed of this and then the * other comparator * @throws NullPointerException if the argument is null. * @since 1.8 */ // 先进行compare比较后，再进行一次比较 default Comparator<T> thenComparing(Comparator<? super T> other) { Objects.requireNonNull(other); return (Comparator<T> & Serializable) (c1, c2) -> { int res = compare(c1, c2); return (res != 0) ? res : other.compare(c1, c2); }; } /** * Returns a lexicographic-order comparator with a function that * extracts a key to be compared with the given {@code Comparator}. * * @implSpec This default implementation behaves as if {@code * thenComparing(comparing(keyExtractor, cmp))}. * * @param <U> the type of the sort key * @param keyExtractor the function used to extract the sort key * @param keyComparator the {@code Comparator} used to compare the sort key * @return a lexicographic-order comparator composed of this comparator * and then comparing on the key extracted by the keyExtractor function * @throws NullPointerException if either argument is null. * @see #comparing(Function, Comparator) * @see #thenComparing(Comparator) * @since 1.8 */ default <U> Comparator<T> thenComparing( Function<? super T, ? extends U> keyExtractor, Comparator<? super U> keyComparator) { return thenComparing(comparing(keyExtractor, keyComparator)); } /** * Returns a lexicographic-order comparator with a function that * extracts a {@code Comparable} sort key. * * @implSpec This default implementation behaves as if {@code * thenComparing(comparing(keyExtractor))}. * * @param <U> the type of the {@link Comparable} sort key * @param keyExtractor the function used to extract the {@link * Comparable} sort key * @return a lexicographic-order comparator composed of this and then the * {@link Comparable} sort key. * @throws NullPointerException if the argument is null. * @see #comparing(Function) * @see #thenComparing(Comparator) * @since 1.8 */ default <U extends Comparable<? super U>> Comparator<T> thenComparing( Function<? super T, ? extends U> keyExtractor) { return thenComparing(comparing(keyExtractor)); } /** * Returns a lexicographic-order comparator with a function that * extracts a {@code int} sort key. * * @implSpec This default implementation behaves as if {@code * thenComparing(comparingInt(keyExtractor))}. * * @param keyExtractor the function used to extract the integer sort key * @return a lexicographic-order comparator composed of this and then the * {@code int} sort key * @throws NullPointerException if the argument is null. * @see #comparingInt(ToIntFunction) * @see #thenComparing(Comparator) * @since 1.8 */ default Comparator<T> thenComparingInt(ToIntFunction<? super T> keyExtractor) { return thenComparing(comparingInt(keyExtractor)); } /** * Returns a lexicographic-order comparator with a function that * extracts a {@code long} sort key. * * @implSpec This default implementation behaves as if {@code * thenComparing(comparingLong(keyExtractor))}. * * @param keyExtractor the function used to extract the long sort key * @return a lexicographic-order comparator composed of this and then the * {@code long} sort key * @throws NullPointerException if the argument is null. * @see #comparingLong(ToLongFunction) * @see #thenComparing(Comparator) * @since 1.8 */ default Comparator<T> thenComparingLong(ToLongFunction<? super T> keyExtractor) { return thenComparing(comparingLong(keyExtractor)); } /** * Returns a lexicographic-order comparator with a function that * extracts a {@code double} sort key. * * @implSpec This default implementation behaves as if {@code * thenComparing(comparingDouble(keyExtractor))}. * * @param keyExtractor the function used to extract the double sort key * @return a lexicographic-order comparator composed of this and then the * {@code double} sort key * @throws NullPointerException if the argument is null. * @see #comparingDouble(ToDoubleFunction) * @see #thenComparing(Comparator) * @since 1.8 */ default Comparator<T> thenComparingDouble(ToDoubleFunction<? super T> keyExtractor) { return thenComparing(comparingDouble(keyExtractor)); } /** * Returns a comparator that imposes the reverse of the <em>natural * ordering</em>. * * <p>The returned comparator is serializable and throws {@link * NullPointerException} when comparing {@code null}. * * @param <T> the {@link Comparable} type of element to be compared * @return a comparator that imposes the reverse of the <i>natural * ordering</i> on {@code Comparable} objects. * @see Comparable * @since 1.8 */ public static <T extends Comparable<? super T>> Comparator<T> reverseOrder() { return Collections.reverseOrder(); } /** * Returns a comparator that compares {@link Comparable} objects in natural * order. * * <p>The returned comparator is serializable and throws {@link * NullPointerException} when comparing {@code null}. * * @param <T> the {@link Comparable} type of element to be compared * @return a comparator that imposes the <i>natural ordering</i> on {@code * Comparable} objects. * @see Comparable * @since 1.8 */ // 返回正常顺序的比较器 @SuppressWarnings("unchecked") public static <T extends Comparable<? super T>> Comparator<T> naturalOrder() { return (Comparator<T>) Comparators.NaturalOrderComparator.INSTANCE; } /** * Returns a null-friendly comparator that considers {@code null} to be * less than non-null. When both are {@code null}, they are considered * equal. If both are non-null, the specified {@code Comparator} is used * to determine the order. If the specified comparator is {@code null}, * then the returned comparator considers all non-null values to be equal. * * <p>The returned comparator is serializable if the specified comparator * is serializable. * * @param <T> the type of the elements to be compared * @param comparator a {@code Comparator} for comparing non-null values * @return a comparator that considers {@code null} to be less than * non-null, and compares non-null objects with the supplied * {@code Comparator}. * @since 1.8 */ public static <T> Comparator<T> nullsFirst(Comparator<? super T> comparator) { return new Comparators.NullComparator<>(true, comparator); } /** * Returns a null-friendly comparator that considers {@code null} to be * greater than non-null. When both are {@code null}, they are considered * equal. If both are non-null, the specified {@code Comparator} is used * to determine the order. If the specified comparator is {@code null}, * then the returned comparator considers all non-null values to be equal. * * <p>The returned comparator is serializable if the specified comparator * is serializable. * * @param <T> the type of the elements to be compared * @param comparator a {@code Comparator} for comparing non-null values * @return a comparator that considers {@code null} to be greater than * non-null, and compares non-null objects with the supplied * {@code Comparator}. * @since 1.8 */ public static <T> Comparator<T> nullsLast(Comparator<? super T> comparator) { return new Comparators.NullComparator<>(false, comparator); } /** * Accepts a function that extracts a sort key from a type {@code T}, and * returns a {@code Comparator<T>} that compares by that sort key using * the specified {@link Comparator}. * * <p>The returned comparator is serializable if the specified function * and comparator are both serializable. * * @apiNote * For example, to obtain a {@code Comparator} that compares {@code * Person} objects by their last name ignoring case differences, * * <pre>{@code * Comparator<Person> cmp = Comparator.comparing( * Person::getLastName, * String.CASE_INSENSITIVE_ORDER); * }</pre> * * @param <T> the type of element to be compared * @param <U> the type of the sort key * @param keyExtractor the function used to extract the sort key * @param keyComparator the {@code Comparator} used to compare the sort key * @return a comparator that compares by an extracted key using the * specified {@code Comparator} * @throws NullPointerException if either argument is null * @since 1.8 */ public static <T, U> Comparator<T> comparing( Function<? super T, ? extends U> keyExtractor, Comparator<? super U> keyComparator) { Objects.requireNonNull(keyExtractor); Objects.requireNonNull(keyComparator); return (Comparator<T> & Serializable) (c1, c2) -> keyComparator.compare(keyExtractor.apply(c1), keyExtractor.apply(c2)); } /** * Accepts a function that extracts a {@link java.lang.Comparable * Comparable} sort key from a type {@code T}, and returns a {@code * Comparator<T>} that compares by that sort key. * * <p>The returned comparator is serializable if the specified function * is also serializable. * * @apiNote * For example, to obtain a {@code Comparator} that compares {@code * Person} objects by their last name, * * <pre>{@code * Comparator<Person> byLastName = Comparator.comparing(Person::getLastName); * }</pre> * * @param <T> the type of element to be compared * @param <U> the type of the {@code Comparable} sort key * @param keyExtractor the function used to extract the {@link * Comparable} sort key * @return a comparator that compares by an extracted key * @throws NullPointerException if the argument is null * @since 1.8 */ public static <T, U extends Comparable<? super U>> Comparator<T> comparing( Function<? super T, ? extends U> keyExtractor) { Objects.requireNonNull(keyExtractor); return (Comparator<T> & Serializable) (c1, c2) -> keyExtractor.apply(c1).compareTo(keyExtractor.apply(c2)); } /** * Accepts a function that extracts an {@code int} sort key from a type * {@code T}, and returns a {@code Comparator<T>} that compares by that * sort key. * * <p>The returned comparator is serializable if the specified function * is also serializable. * * @param <T> the type of element to be compared * @param keyExtractor the function used to extract the integer sort key * @return a comparator that compares by an extracted key * @see #comparing(Function) * @throws NullPointerException if the argument is null * @since 1.8 */ // 对int类型的key进行比较 public static <T> Comparator<T> comparingInt(ToIntFunction<? super T> keyExtractor) { Objects.requireNonNull(keyExtractor); return (Comparator<T> & Serializable) (c1, c2) -> Integer.compare(keyExtractor.applyAsInt(c1), keyExtractor.applyAsInt(c2)); } /** * Accepts a function that extracts a {@code long} sort key from a type * {@code T}, and returns a {@code Comparator<T>} that compares by that * sort key. * * <p>The returned comparator is serializable if the specified function is * also serializable. * * @param <T> the type of element to be compared * @param keyExtractor the function used to extract the long sort key * @return a comparator that compares by an extracted key * @see #comparing(Function) * @throws NullPointerException if the argument is null * @since 1.8 */ public static <T> Comparator<T> comparingLong(ToLongFunction<? super T> keyExtractor) { Objects.requireNonNull(keyExtractor); return (Comparator<T> & Serializable) (c1, c2) -> Long.compare(keyExtractor.applyAsLong(c1), keyExtractor.applyAsLong(c2)); } /** * Accepts a function that extracts a {@code double} sort key from a type * {@code T}, and returns a {@code Comparator<T>} that compares by that * sort key. * * <p>The returned comparator is serializable if the specified function * is also serializable. * * @param <T> the type of element to be compared * @param keyExtractor the function used to extract the double sort key * @return a comparator that compares by an extracted key * @see #comparing(Function) * @throws NullPointerException if the argument is null * @since 1.8 */ public static<T> Comparator<T> comparingDouble(ToDoubleFunction<? super T> keyExtractor) { Objects.requireNonNull(keyExtractor); return (Comparator<T> & Serializable) (c1, c2) -> Double.compare(keyExtractor.applyAsDouble(c1), keyExtractor.applyAsDouble(c2)); } }可以看出，Comparator接口中很多方法是JDK1.8增加的，所以在JDK1.8之前很多要自己手动实现Comparator接口，再去调用Collections.sort()，传入实现类来完成排序。下面就是使用的比较：3.7.4 NavigableMap接口先源码解析一遍：public interface NavigableMap<K,V> extends SortedMap<K,V> { /** * Returns a key-value mapping associated with the greatest key * strictly less than the given key, or {@code null} if there is * no such key. * * @param key the key * @return an entry with the greatest key less than {@code key}, * or {@code null} if there is no such key * @throws ClassCastException if the specified key cannot be compared * with the keys currently in the map * @throws NullPointerException if the specified key is null * and this map does not permit null keys */ // 返回键小于且最接近Key（不包含等于）的键值对，没有返回null Map.Entry<K,V> lowerEntry(K key); /** * Returns the greatest key strictly less than the given key, or * {@code null} if there is no such key. * * @param key the key * @return the greatest key less than {@code key}, * or {@code null} if there is no such key * @throws ClassCastException if the specified key cannot be compared * with the keys currently in the map * @throws NullPointerException if the specified key is null * and this map does not permit null keys */ // 返回小于且最接近（不包含等于）Key的键，没有返回null K lowerKey(K key); /** * Returns a key-value mapping associated with the greatest key * less than or equal to the given key, or {@code null} if there * is no such key. * * @param key the key * @return an entry with the greatest key less than or equal to * {@code key}, or {@code null} if there is no such key * @throws ClassCastException if the specified key cannot be compared * with the keys currently in the map * @throws NullPointerException if the specified key is null * and this map does not permit null keys */ // 返回键小于且最接近（包含等于）Key的键值对，没有返回null Map.Entry<K,V> floorEntry(K key); /** * Returns the greatest key less than or equal to the given key, * or {@code null} if there is no such key. * * @param key the key * @return the greatest key less than or equal to {@code key}, * or {@code null} if there is no such key * @throws ClassCastException if the specified key cannot be compared * with the keys currently in the map * @throws NullPointerException if the specified key is null * and this map does not permit null keys */ // 返回小于且最接近（包含等于）Key的键，没有返回null K floorKey(K key); /** * Returns a key-value mapping associated with the least key * greater than or equal to the given key, or {@code null} if * there is no such key. * * @param key the key * @return an entry with the least key greater than or equal to * {@code key}, or {@code null} if there is no such key * @throws ClassCastException if the specified key cannot be compared * with the keys currently in the map * @throws NullPointerException if the specified key is null * and this map does not permit null keys */ // 返回大于且最接近（包含等于）给定key的键值对，没有返回null Map.Entry<K,V> ceilingEntry(K key); /** * Returns the least key greater than or equal to the given key, * or {@code null} if there is no such key. * * @param key the key * @return the least key greater than or equal to {@code key}, * or {@code null} if there is no such key * @throws ClassCastException if the specified key cannot be compared * with the keys currently in the map * @throws NullPointerException if the specified key is null * and this map does not permit null keys */ // 返回大于且最接近（包含等于）给定key的键值对，没有返回null K ceilingKey(K key); /** * Returns a key-value mapping associated with the least key * strictly greater than the given key, or {@code null} if there * is no such key. * * @param key the key * @return an entry with the least key greater than {@code key}, * or {@code null} if there is no such key * @throws ClassCastException if the specified key cannot be compared * with the keys currently in the map * @throws NullPointerException if the specified key is null * and this map does not permit null keys */ // 返回大于且最接近（不包含等于）给定key的键值对 Map.Entry<K,V> higherEntry(K key); /** * Returns the least key strictly greater than the given key, or * {@code null} if there is no such key. * * @param key the key * @return the least key greater than {@code key}, * or {@code null} if there is no such key * @throws ClassCastException if the specified key cannot be compared * with the keys currently in the map * @throws NullPointerException if the specified key is null * and this map does not permit null keys */ // 返回大于且最接近（不包含等于）给定key的键值对 K higherKey(K key); /** * Returns a key-value mapping associated with the least * key in this map, or {@code null} if the map is empty. * * @return an entry with the least key, * or {@code null} if this map is empty */ // 返回第一个Entry Map.Entry<K,V> firstEntry(); /** * Returns a key-value mapping associated with the greatest * key in this map, or {@code null} if the map is empty. * * @return an entry with the greatest key, * or {@code null} if this map is empty */ // 返回最后一个Entry Map.Entry<K,V> lastEntry(); /** * Removes and returns a key-value mapping associated with * the least key in this map, or {@code null} if the map is empty. * * @return the removed first entry of this map, * or {@code null} if this map is empty */ // 移除并返回第一个Entry Map.Entry<K,V> pollFirstEntry(); /** * Removes and returns a key-value mapping associated with * the greatest key in this map, or {@code null} if the map is empty. * * @return the removed last entry of this map, * or {@code null} if this map is empty */ // 移除并返回第一个Entry Map.Entry<K,V> pollLastEntry(); /** * Returns a reverse order view of the mappings contained in this map. * The descending map is backed by this map, so changes to the map are * reflected in the descending map, and vice-versa. If either map is * modified while an iteration over a collection view of either map * is in progress (except through the iterator's own {@code remove} * operation), the results of the iteration are undefined. * * <p>The returned map has an ordering equivalent to * <tt>{@link Collections#reverseOrder(Comparator) Collections.reverseOrder}(comparator())</tt>. * The expression {@code m.descendingMap().descendingMap()} returns a * view of {@code m} essentially equivalent to {@code m}. * * @return a reverse order view of this map */ // 返回map中包含的映射关系的逆序视图 NavigableMap<K,V> descendingMap(); /** * Returns a {@link NavigableSet} view of the keys contained in this map. * The set's iterator returns the keys in ascending order. * The set is backed by the map, so changes to the map are reflected in * the set, and vice-versa. If the map is modified while an iteration * over the set is in progress (except through the iterator's own {@code * remove} operation), the results of the iteration are undefined. The * set supports element removal, which removes the corresponding mapping * from the map, via the {@code Iterator.remove}, {@code Set.remove}, * {@code removeAll}, {@code retainAll}, and {@code clear} operations. * It does not support the {@code add} or {@code addAll} operations. * * @return a navigable set view of the keys in this map */ // 返回map中包含的键的NavigableSet视图。 set的迭代器按key的升序 NavigableSet<K> navigableKeySet(); /** * Returns a reverse order {@link NavigableSet} view of the keys contained in this map. * The set's iterator returns the keys in descending order. * The set is backed by the map, so changes to the map are reflected in * the set, and vice-versa. If the map is modified while an iteration * over the set is in progress (except through the iterator's own {@code * remove} operation), the results of the iteration are undefined. The * set supports element removal, which removes the corresponding mapping * from the map, via the {@code Iterator.remove}, {@code Set.remove}, * {@code removeAll}, {@code retainAll}, and {@code clear} operations. * It does not support the {@code add} or {@code addAll} operations. * * @return a reverse order navigable set view of the keys in this map */ // 逆序 NavigableSet<K> descendingKeySet(); /** * Returns a view of the portion of this map whose keys range from * {@code fromKey} to {@code toKey}. If {@code fromKey} and * {@code toKey} are equal, the returned map is empty unless * {@code fromInclusive} and {@code toInclusive} are both true. The * returned map is backed by this map, so changes in the returned map are * reflected in this map, and vice-versa. The returned map supports all * optional map operations that this map supports. * * <p>The returned map will throw an {@code IllegalArgumentException} * on an attempt to insert a key outside of its range, or to construct a * submap either of whose endpoints lie outside its range. * * @param fromKey low endpoint of the keys in the returned map * @param fromInclusive {@code true} if the low endpoint * is to be included in the returned view * @param toKey high endpoint of the keys in the returned map * @param toInclusive {@code true} if the high endpoint * is to be included in the returned view * @return a view of the portion of this map whose keys range from * {@code fromKey} to {@code toKey} * @throws ClassCastException if {@code fromKey} and {@code toKey} * cannot be compared to one another using this map's comparator * (or, if the map has no comparator, using natural ordering). * Implementations may, but are not required to, throw this * exception if {@code fromKey} or {@code toKey} * cannot be compared to keys currently in the map. * @throws NullPointerException if {@code fromKey} or {@code toKey} * is null and this map does not permit null keys * @throws IllegalArgumentException if {@code fromKey} is greater than * {@code toKey}; or if this map itself has a restricted * range, and {@code fromKey} or {@code toKey} lies * outside the bounds of the range */ // 根据fromKey和toKey来返回子map，两个boolean参数用于是否包含该key NavigableMap<K,V> subMap(K fromKey, boolean fromInclusive, K toKey, boolean toInclusive); /** * Returns a view of the portion of this map whose keys are less than (or * equal to, if {@code inclusive} is true) {@code toKey}. The returned * map is backed by this map, so changes in the returned map are reflected * in this map, and vice-versa. The returned map supports all optional * map operations that this map supports. * * <p>The returned map will throw an {@code IllegalArgumentException} * on an attempt to insert a key outside its range. * * @param toKey high endpoint of the keys in the returned map * @param inclusive {@code true} if the high endpoint * is to be included in the returned view * @return a view of the portion of this map whose keys are less than * (or equal to, if {@code inclusive} is true) {@code toKey} * @throws ClassCastException if {@code toKey} is not compatible * with this map's comparator (or, if the map has no comparator, * if {@code toKey} does not implement {@link Comparable}). * Implementations may, but are not required to, throw this * exception if {@code toKey} cannot be compared to keys * currently in the map. * @throws NullPointerException if {@code toKey} is null * and this map does not permit null keys * @throws IllegalArgumentException if this map itself has a * restricted range, and {@code toKey} lies outside the * bounds of the range */ // 返回小于（或等于,根据inclusive）toKey的map NavigableMap<K,V> headMap(K toKey, boolean inclusive); /** * Returns a view of the portion of this map whose keys are greater than (or * equal to, if {@code inclusive} is true) {@code fromKey}. The returned * map is backed by this map, so changes in the returned map are reflected * in this map, and vice-versa. The returned map supports all optional * map operations that this map supports. * * <p>The returned map will throw an {@code IllegalArgumentException} * on an attempt to insert a key outside its range. * * @param fromKey low endpoint of the keys in the returned map * @param inclusive {@code true} if the low endpoint * is to be included in the returned view * @return a view of the portion of this map whose keys are greater than * (or equal to, if {@code inclusive} is true) {@code fromKey} * @throws ClassCastException if {@code fromKey} is not compatible * with this map's comparator (or, if the map has no comparator, * if {@code fromKey} does not implement {@link Comparable}). * Implementations may, but are not required to, throw this * exception if {@code fromKey} cannot be compared to keys * currently in the map. * @throws NullPointerException if {@code fromKey} is null * and this map does not permit null keys * @throws IllegalArgumentException if this map itself has a * restricted range, and {@code fromKey} lies outside the * bounds of the range */ // 返回大于（或等于,根据inclusive）fromKey的map NavigableMap<K,V> tailMap(K fromKey, boolean inclusive); /** * {@inheritDoc} * * <p>Equivalent to {@code subMap(fromKey, true, toKey, false)}. * * @throws ClassCastException {@inheritDoc} * @throws NullPointerException {@inheritDoc} * @throws IllegalArgumentException {@inheritDoc} */ SortedMap<K,V> subMap(K fromKey, K toKey); /** * {@inheritDoc} * * <p>Equivalent to {@code headMap(toKey, false)}. * * @throws ClassCastException {@inheritDoc} * @throws NullPointerException {@inheritDoc} * @throws IllegalArgumentException {@inheritDoc} */ SortedMap<K,V> headMap(K toKey); /** * {@inheritDoc} * * <p>Equivalent to {@code tailMap(fromKey, true)}. * * @throws ClassCastException {@inheritDoc} * @throws NullPointerException {@inheritDoc} * @throws IllegalArgumentException {@inheritDoc} */ SortedMap<K,V> tailMap(K fromKey); }注意：上述返回的map与原map是相互影响的。3.7.5 TreeMap结构TreeMap的底层是红黑树，所以它的结构如下图：红黑树定义：1. 节点是红色或黑色。2. 根是黑色。3. 所有叶子都是黑色（叶子是NIL节点）。4. 每个红色节点必须有两个黑色的子节点。（从每个叶子到根的所有路径上不能有两个连续的红色节点。）5. 从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点。Entry类：除了key-value属性，还有该节点的左节点left，右节点right，父节点parent。 /** * Node in the Tree. Doubles as a means to pass key-value pairs back to * user (see Map.Entry). */ static final class Entry<K,V> implements Map.Entry<K,V> { K key; V value; Entry<K,V> left; Entry<K,V> right; Entry<K,V> parent; boolean color = BLACK; /** * Make a new cell with given key, value, and parent, and with * {@code null} child links, and BLACK color. */ Entry(K key, V value, Entry<K,V> parent) { this.key = key; this.value = value; this.parent = parent; } /** * Returns the key. * * @return the key */ public K getKey() { return key; } /** * Returns the value associated with the key. * * @return the value associated with the key */ public V getValue() { return value; } /** * Replaces the value currently associated with the key with the given * value. * * @return the value associated with the key before this method was * called */ public V setValue(V value) { V oldValue = this.value; this.value = value; return oldValue; } public boolean equals(Object o) { if (!(o instanceof Map.Entry)) return false; Map.Entry<?,?> e = (Map.Entry<?,?>)o; return valEquals(key,e.getKey()) && valEquals(value,e.getValue()); } public int hashCode() { int keyHash = (key==null ? 0 : key.hashCode()); int valueHash = (value==null ? 0 : value.hashCode()); return keyHash ^ valueHash; } public String toString() { return key + "=" + value; } }3.7.5 TreeMap成员变量// Key的比较器，用作排序 private final Comparator<? super K> comparator; // 树的根节点 private transient Entry<K,V> root; // 树的大小 private transient int size = 0; // 修改计数器 private transient int modCount = 0; // 返回map的Entry视图 private transient EntrySet entrySet; private transient KeySet<K> navigableKeySet; private transient NavigableMap<K,V> descendingMap; // 定义红黑树的颜色 private static final boolean RED = false; private static final boolean BLACK = true;3.7.6 构造方法TreeMap(Comparator<? super K>)public TreeMap(Comparator<? super K> comparator) { this.comparator = comparator; }允许用户自定义比较器进行key的排序。TreeMap(Map<? extends K, ? extends V>)public TreeMap(Map<? extends K, ? extends V> m) { comparator = null; putAll(m); } public void putAll(Map<? extends K, ? extends V> map) { int mapSize = map.size(); // 判断map是否SortedMap，不是则采用AbstractMap的putAll if (size==0 && mapSize!=0 && map instanceof SortedMap) { Comparator<?> c = ((SortedMap<?,?>)map).comparator(); // 同为null或者不为null，类型相同，则进入有序map的构造 if (c == comparator || (c != null && c.equals(comparator))) { ++modCount; try { buildFromSorted(mapSize, map.entrySet().iterator(), null, null); } catch (java.io.IOException cannotHappen) { } catch (ClassNotFoundException cannotHappen) { } return; } } super.putAll(map); }根据key的自然排序将参数中m的元素存储到treeMap中TreeMap(SortedMap<K, ? extends V>)public TreeMap(SortedMap<K, ? extends V> m) { comparator = m.comparator(); try { buildFromSorted(m.size(), m.entrySet().iterator(), null, null); } catch (java.io.IOException cannotHappen) { } catch (ClassNotFoundException cannotHappen) { } }根据sortedMap中比较器的排序规则将参数中m的元素存储到treeMap中。buildFromSorted 方法的源码：/** * Linear time tree building algorithm from sorted data. Can accept keys * and/or values from iterator or stream. This leads to too many * parameters, but seems better than alternatives. The four formats * that this method accepts are: * * 1) An iterator of Map.Entries. (it != null, defaultVal == null). * 2) An iterator of keys. (it != null, defaultVal != null). * 3) A stream of alternating serialized keys and values. * (it == null, defaultVal == null). * 4) A stream of serialized keys. (it == null, defaultVal != null). * * It is assumed that the comparator of the TreeMap is already set prior * to calling this method. * * @param size the number of keys (or key-value pairs) to be read from * the iterator or stream * @param it If non-null, new entries are created from entries * or keys read from this iterator. * @param str If non-null, new entries are created from keys and * possibly values read from this stream in serialized form. * Exactly one of it and str should be non-null. * @param defaultVal if non-null, this default value is used for * each value in the map. If null, each value is read from * iterator or stream, as described above. * @throws java.io.IOException propagated from stream reads. This cannot * occur if str is null. * @throws ClassNotFoundException propagated from readObject. * This cannot occur if str is null. * * size: map里键值对的数量 * it: 传入的map的entries迭代器 * str: 如果不为空，则从流里读取key-value * defaultVal：见名知意，不为空，则value都用这个值 */ private void buildFromSorted(int size, Iterator<?> it, java.io.ObjectInputStream str, V defaultVal) throws java.io.IOException, ClassNotFoundException { this.size = size; root = buildFromSorted(0, 0, size-1, computeRedLevel(size), it, str, defaultVal); } private static int computeRedLevel(int sz) { int level = 0; for (int m = sz - 1; m >= 0; m = m / 2 - 1) level++; return level; } /** * Recursive "helper method" that does the real work of the * previous method. Identically named parameters have * identical definitions. Additional parameters are documented below. * It is assumed that the comparator and size fields of the TreeMap are * already set prior to calling this method. (It ignores both fields.) * * @param level the current level of tree. Initial call should be 0. * @param lo the first element index of this subtree. Initial should be 0. * @param hi the last element index of this subtree. Initial should be * size-1. * @param redLevel the level at which nodes should be red. * Must be equal to computeRedLevel for tree of this size. * * level: 当前树的层数，注意：是从0层开始 * lo: 子树第一个元素的索引 * hi: 子树最后一个元素的索引 * redLevel: 上述红节点所在层数 * 剩下的3个就不解释了，跟上面的一样 */ @SuppressWarnings("unchecked") private final Entry<K,V> buildFromSorted(int level, int lo, int hi, int redLevel, Iterator<?> it, java.io.ObjectInputStream str, V defaultVal) throws java.io.IOException, ClassNotFoundException { /* * Strategy: The root is the middlemost element. To get to it, we * have to first recursively construct the entire left subtree, * so as to grab all of its elements. We can then proceed with right * subtree. * * The lo and hi arguments are the minimum and maximum * indices to pull out of the iterator or stream for current subtree. * They are not actually indexed, we just proceed sequentially, * ensuring that items are extracted in corresponding order. */ // hi >= lo 说明子树已经构造完成 if (hi < lo) return null; // 取中间位置，无符号右移，相当于除2 int mid = (lo + hi) >>> 1; Entry<K,V> left = null; // 递归构造左结点 if (lo < mid) left = buildFromSorted(level+1, lo, mid - 1, redLevel, it, str, defaultVal); // extract key and/or value from iterator or stream K key; V value; // 通过迭代器获取key， value if (it != null) { if (defaultVal==null) { Map.Entry<?,?> entry = (Map.Entry<?,?>)it.next(); key = (K)entry.getKey(); value = (V)entry.getValue(); } else { key = (K)it.next(); value = defaultVal; } // 通过流来读取key, value } else { // use stream key = (K) str.readObject(); value = (defaultVal != null ? defaultVal : (V) str.readObject()); } // 构建结点 Entry<K,V> middle = new Entry<>(key, value, null); // level从0开始的，所以上述9个节点，计算出来的是3，实际上就是代表的第4层 // color nodes in non-full bottommost level red if (level == redLevel) middle.color = RED; // 如果存在的话，设置左结点， if (left != null) { middle.left = left; left.parent = middle; } // 递归构造右结点 if (mid < hi) { Entry<K,V> right = buildFromSorted(level+1, mid+1, hi, redLevel, it, str, defaultVal); middle.right = right; right.parent = middle; } return middle; }它的作用是用来计算完全二叉树的层数。什么意思呢，先来看一下下面的图：把根结点索引看为0，那么高度为2的树的最后一个节点的索引为2，类推高度为3的最后一个节点为6，满足m = (m + 1) * 2。那么计算这个高度有什么好处呢，如上图，如果一个树有9个节点，那么我们构造红黑树的时候，只要把前面3层的结点都设置为黑色，第四层的节点设置为红色，则构造完的树，就是红黑树，满足前面提到的红黑树的5个条件。而实现的关键就是找到要构造树的完全二叉树的层数。buildFromSorted能这么构造是因为这是一个已经排序的map。构造顺序图如下：3.7.7 get方法源码分析： public V get(Object key) { Entry<K,V> p = getEntry(key); return (p==null ? null : p.value); } final Entry<K,V> getEntry(Object key) { // Offload comparator-based version for sake of performance // 如果有比较器，则调用通过比较器的来比较key的方法 if (comparator != null) // 根据自定义的比较器的排序规则获取节点，把compareTo变成了用Comparator进行比较 return getEntryUsingComparator(key); if (key == null) throw new NullPointerException(); @SuppressWarnings("unchecked") // 获取key的Comparable接口 Comparable<? super K> k = (Comparable<? super K>) key; // 从根结点开始比较，根据二叉树的形式，小的往左树找，大的往右树找，直到找到返回 Entry<K,V> p = root; // 比较器为null，通过key的循环比较获取节点 while (p != null) { int cmp = k.compareTo(p.key); if (cmp < 0) p = p.left; else if (cmp > 0) p = p.right; else return p; } return null; } final Entry<K,V> getEntryUsingComparator(Object key) { @SuppressWarnings("unchecked") K k = (K) key; Comparator<? super K> cpr = comparator; if (cpr != null) { Entry<K,V> p = root; while (p != null) { int cmp = cpr.compare(k, p.key); if (cmp < 0) p = p.left; else if (cmp > 0) p = p.right; else return p; } } return null; }3.7.8 put方法put方法较为复杂，先看看源码：public V put(K key, V value) { // 将根节点赋值给t Entry<K,V> t = root; // 根结点为空，则进行添加根结点并初始化参数 if (t == null) { // 用来进行类型检查 compare(key, key); // type (and possibly null) check // 将第一个元素赋值给根节点 root = new Entry<>(key, value, null); size = 1; modCount++; return null; } int cmp; // 定义比较结果 Entry<K,V> parent; // 定义put进来的元素的父节点 // split comparator and comparable paths // 与get类型，分离comparator与comparable的比较 Comparator<? super K> cpr = comparator; if (cpr != null) { // 循环查找key，如果找到则替换value，没有则记录其parent，后面进行插入 do { parent = t; // 获取要存储元素的parent节点 // 从root开始，比较两者key的大小 cmp = cpr.compare(key, t.key); if (cmp < 0) // 小于已存在节点的key，将t.left赋值给t，以便再次进行比较 t = t.left; else if (cmp > 0) // 大于已存在节点的key，将t.right赋值给t,以便再次进行比较 t = t.right; else // 为0，表示两者相等，用value替换原value值，并返回原value return t.setValue(value); } while (t != null); // t != null，接着进行比较 } else { if (key == null) throw new NullPointerException(); @SuppressWarnings("unchecked") // 获取key的compareTo方法 Comparable<? super K> k = (Comparable<? super K>) key; do { parent = t; // 获取要存储元素的parent节点 // 从root开始，比较两者key的大小 cmp = k.compareTo(t.key); // 同上 if (cmp < 0) t = t.left; else if (cmp > 0) t = t.right; else return t.setValue(value); } while (t != null); } // 创建结点，然后比较与parent的大小，小放在左结点，大放在右节点 Entry<K,V> e = new Entry<>(key, value, parent); if (cmp < 0) // 小于0，位于parent的左边 parent.left = e; else // 大于0，位于parent元素的右边 parent.right = e; // 插入新节点可能会破坏红黑树性质，插入后进行修正（对红黑树进行修复） fixAfterInsertion(e); size++; modCount++; return null; }这里当往TreeMap放入新的键值对后，可能会破坏红黑树的性质，为了方便描述，把 Entry 称为节点。并把新插入的节点称为N，N 的父节点为P。P 的父节点为G，且 P 是 G 的左孩子。P 的兄弟节点为U。在往红黑树中插入新的节点 N 后（新节点为红色），会产生下面5种情况：1. N 是根节点2. N 的父节点是黑色3. N 的父节点是红色，叔叔节点也是红色4. N 的父节点是红色，叔叔节点是黑色，且 N 是 P 的右孩子5. N 的父节点是红色，叔叔节点是黑色，且 N 是 P 的左孩子上面5中情况中，情况2不会破坏红黑树性质，所以无需处理。情况1 会破坏红黑树性质2（根是黑色），情况3、4、和5会破坏红黑树性质4（每个红色节点必须有两个黑色的子节点），这时需要fixAfterInsertion方法对红黑树进行修复接下来看看代码最后fixAfterInsertion方法源码：/** From CLR */ private void fixAfterInsertion(Entry<K,V> x) { // 约定插入的结点都是红节点 x.color = RED; // x本身红色，如果其父节点也是红色，违反规则4，进行循环处理 while (x != null && x != root && x.parent.color == RED) { // 父节点是左结点 if (parentOf(x) == leftOf(parentOf(parentOf(x)))) { // 获取父节点的右兄弟y Entry<K,V> y = rightOf(parentOf(parentOf(x))); // p为左结点，y为红色 ① if (colorOf(y) == RED) { setColor(parentOf(x), BLACK); setColor(y, BLACK); setColor(parentOf(parentOf(x)), RED); x = parentOf(parentOf(x)); } else { // p为左结点，y为黑，x为右节点 ② if (x == rightOf(parentOf(x))) { x = parentOf(x); rotateLeft(x); } // p为左结点，y为红，x为左结点 ③ setColor(parentOf(x), BLACK); setColor(parentOf(parentOf(x)), RED); rotateRight(parentOf(parentOf(x))); } // 父节点是右结点 } else { Entry<K,V> y = leftOf(parentOf(parentOf(x))); // p为右结点，y为红色 ④ if (colorOf(y) == RED) { setColor(parentOf(x), BLACK); setColor(y, BLACK); setColor(parentOf(parentOf(x)), RED); x = parentOf(parentOf(x)); } else { // p为右结点，y为黑色，x为左结点 ⑤ if (x == leftOf(parentOf(x))) { x = parentOf(x); rotateRight(x); } // p为右结点，y为黑色，x为右结点 ⑥ setColor(parentOf(x), BLACK); setColor(parentOf(parentOf(x)), RED); rotateLeft(parentOf(parentOf(x))); } } } // 约定根结点都是黑节点 root.color = BLACK; }下面是图片和代码的结合，图片转载自参考12。3.7.9 remove方法删除是最复杂的，原因是该操作可能会破坏红黑树性质5（从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点），修复性质5要比修复其他性质（性质2和4需修复，性质1和3不用修复）复杂的多。首先看看remove的源码：public V remove(Object key) { // 获取Entry Entry<K,V> p = getEntry(key); if (p == null) return null; V oldValue = p.value; // 删除Entry deleteEntry(p); return oldValue; }getEntry在get方法中就有讲解，不懂的可以回头看看，下面讲解一下修复。当删除操作导致性质5被破坏时，会出现8种情况。为了方便表述，这里还是先做一些假设。我们把最终被删除的节点称为 X，X 的替换节点称为 N。N 的父节点为P，且 N 是 P 的左孩子。N 的兄弟节点为S，S 的左孩子为 SL，右孩子为 SR。这里特地强调 X 是 最终被删除 的节点，是原因二叉查找树会把要删除有两个孩子的节点的情况转化为删除只有一个孩子的节点的情况，该节点是欲被删除节点的前驱和后继。接下来，简单列举一下删除节点时可能会出现的情况，先列举较为简单的情况：1. 最终被删除的节点 X 是红色节点2. X 是黑色节点，但该节点的孩子节点是红色比较复杂的情况：1. 替换节点 N 是新的根2. N 为黑色，N 的兄弟节点 S 为红色，其他节点为黑色。3. N 为黑色，N 的父节点 P，兄弟节点 S 和 S 的孩子节点均为黑色。4. N 为黑色，P 是红色，S 和 S 孩子均为黑色。5. N 为黑色，P 可红可黑，S 为黑色，S 的左孩子 SL 为红色，右孩子 SR 为黑色6. N 为黑色，P 可红可黑，S 为黑色，SR 为红色，SL 可红可黑下面是deleteEntry这个remove中的核心方法，先看一下源码：/** * Delete node p, and then rebalance the tree. */ private void deleteEntry(Entry<K,V> p) { modCount++; size--; // If strictly internal, copy successor's element to p and then make p // point to successor. /* * 1. 如果 p 有两个孩子节点，则找到后继节点， * 并把后继节点的值复制到节点 P 中，并让 p 指向其后继节点 * （p的左右子树都不为空，找到右子树中最小的结点，将key、value赋给p，然后p指向后继结点） */ if (p.left != null && p.right != null) { Entry<K,V> s = successor(p); p.key = s.key; p.value = s.value; p = s; } // p has 2 children // 获取p中不为空的结点，也可能两个都是空的 // Start fixup at replacement node, if it exists. Entry<K,V> replacement = (p.left != null ? p.left : p.right); // 替换的结点有一个子节点 if (replacement != null) { // Link replacement to parent /* * 2. 将 replacement parent 引用指向新的父节点， * 同时让新的父节点指向 replacement。 */ replacement.parent = p.parent; if (p.parent == null) root = replacement; else if (p == p.parent.left) p.parent.left = replacement; else p.parent.right = replacement; // 清空链接，以便可以使用fixAfterDeletion和内存回收 // Null out links so they are OK to use by fixAfterDeletion. p.left = p.right = p.parent = null; // Fix replacement // 3. 如果删除的节点 p 是黑色节点，则需要进行调整 if (p.color == BLACK) fixAfterDeletion(replacement); } else if (p.parent == null) { // return if we are the only node. // 删除的是根节点，且树中当前只有一个节点 root = null; } else { // No children. Use self as phantom replacement and unlink. // 删除的节点没有孩子节点（空节点） // p 是黑色，则需要进行调整 if (p.color == BLACK) fixAfterDeletion(p); // 将 P 从树中移除 if (p.parent != null) { if (p == p.parent.left) // 清空链接，方便GC p.parent.left = null; else if (p == p.parent.right) p.parent.right = null; // 清空链接，方便GC p.parent = null; } } }deleteEntry 主要做了这么几件事：1. 如果待删除节点 P 有两个孩子，则先找到 P 的后继 S，然后将 S 中的值拷贝到 P 中，并让 P 指向 S2. 如果最终被删除节点 P（P 现在指向最终被删除节点）的孩子不为空，则用其孩子节点替换掉3. 如果最终被删除的节点是黑色的话，调用 fixAfterDeletion 方法进行修复上面说了 replacement 不为空时，deleteEntry 的执行逻辑。上面说的略微啰嗦，如果简单说的话，7个字即可总结：找后继 -> 替换 -> 修复。修复就是fixAfterDeletion这个方法，在看fixAfter之前先看看successor方法：successor方法源码解析：/** * Returns the successor of the specified Entry, or null if no such. */ // 查找t的后继结点 static <K,V> TreeMap.Entry<K,V> successor(Entry<K,V> t) { if (t == null) return null; // 从t的右子树中找到最小的 else if (t.right != null) { Entry<K,V> p = t.right; while (p.left != null) p = p.left; return p; // 当右子树为空时，向上找到第一个左父节点 } else { Entry<K,V> p = t.parent; Entry<K,V> ch = t; while (p != null && ch == p.right) { ch = p; p = p.parent; } return p; } }从源码可以看出，它实现了找到最接近且大于t的节点，这样的话，直接用来替换掉t，对原有的树的结构变动最小。fixAfterDeletion方法源码解析： /** From CLR */ private void fixAfterDeletion(Entry<K,V> x) { while (x != root && colorOf(x) == BLACK) { // x是左结点且为黑色 if (x == leftOf(parentOf(x))) { // 获取兄弟右节点 Entry<K,V> sib = rightOf(parentOf(x)); // ① 兄弟右节点sib颜色是红色 if (colorOf(sib) == RED) { setColor(sib, BLACK); setColor(parentOf(x), RED); rotateLeft(parentOf(x)); sib = rightOf(parentOf(x)); } // ② sib的子节点都是黑色 if (colorOf(leftOf(sib)) == BLACK && colorOf(rightOf(sib)) == BLACK) { setColor(sib, RED); x = parentOf(x); // sib子节点不全为黑 } else { // ③ sib右子节点为黑色 if (colorOf(rightOf(sib)) == BLACK) { setColor(leftOf(sib), BLACK); setColor(sib, RED); rotateRight(sib); sib = rightOf(parentOf(x)); } // ④ setColor(sib, colorOf(parentOf(x))); setColor(parentOf(x), BLACK); setColor(rightOf(sib), BLACK); rotateLeft(parentOf(x)); x = root; } // 对称 } else { // symmetric Entry<K,V> sib = leftOf(parentOf(x)); if (colorOf(sib) == RED) { setColor(sib, BLACK); setColor(parentOf(x), RED); rotateRight(parentOf(x)); sib = leftOf(parentOf(x)); } if (colorOf(rightOf(sib)) == BLACK && colorOf(leftOf(sib)) == BLACK) { setColor(sib, RED); x = parentOf(x); } else { if (colorOf(leftOf(sib)) == BLACK) { setColor(rightOf(sib), BLACK); setColor(sib, RED); rotateLeft(sib); sib = leftOf(parentOf(x)); } setColor(sib, colorOf(parentOf(x))); setColor(parentOf(x), BLACK); setColor(leftOf(sib), BLACK); rotateRight(parentOf(x)); x = root; } } } setColor(x, BLACK); }具体原理可以先看完红黑树再来看，不多讲解了。下面是图文结合，图片转载自参考12：建议还是先看完红黑树再来看这篇文章，红黑树一文讲解的理论层面上的详细分析红黑树的源码，而这里就是在实践层面上对红黑树进行了解刨。3.8 Hashtable、ConcurrentHashMap、HashMap、LinkedHashMap、TreeMap区别下面以问题的形式：3.8.1 HashMap、HashTable、ConcurrentHashMap区别？从容器整体结构HashMap的key和value都允许为null，HashMap遇到key为null的时候，调用putForNullKey方法进行处理，而对value没有处理。Hashtable和ConcurrentHashMap的key和value都不允许为null。Hashtable遇到null，直接返回NullPointerException。从容量设定和扩容机制HashMap和ConcurrentHashMap默认初始化容量为 16，并且容器容量一定是2的n次方，扩容时，是以原容量 2倍 的方式 进行扩容。Hashtable默认初始化容量为 11，扩容时，是以原容量 2倍 再加 1的方式进行扩容。即int newCapacity = (oldCapacity << 1) + 1;。散列分布方式（计算存储位置）HashMap和ConcurrentHashMap是是先将key键的hashCode经过扰动函数扰动后得到hash值，然后再利用 hash & (length - 1)的方式代替取模，得到元素的存储位置。Hashtable则是除留余数法进行计算存储位置的（因为其默认容量也不是2的n次方。所以也无法用位运算替代模运算），int index = (hash & 0x7FFFFFFF) % tab.length;。由于HashMap和ConcurrentHashMap的容器容量一定是2的n次方，所以能使用hash & (length - 1)的方式代替取模的方式计算元素的位置提高运算效率，但Hashtable的容器容量不一定是2的n次方，所以不能使用此运算方式代替。线程安全（最重要）HashMap 不是线程安全，如果想线程安全，可以通过调用synchronizedMap(Map<K,V> m)使其线程安全。但是使用时的运行效率会下降，所以建议使用ConcurrentHashMap容器以此达到线程安全。Hashtable则是线程安全的，每个操作方法前都有synchronized修饰使其同步，但运行效率也不高，所以还是建议使用ConcurrentHashMap容器以此达到线程安全。ConcurrentHashMap也是线程安全的，但是相比较于Hashtable，ConcurrentHashMap的效率更高。3.8.2 LinkedHashMap、HashMap、TreeMap区别？1. LinkedHashMap是继承自HashMap，是基于HashMap和双链表实现的。2. HashMap是无序的，LinkedHashMap是有序，可分为插入顺序和访问顺序两种。3. LinkedHashMap存取数据还是与HashMap一样，只是它需要维护双向链表去保证顺序。4. LinkedHashMap、HashMap和TreeMap都是线程不安全的。5. TreeMap 将根据它们的 compareTo() 方法(或外部提供的比较器)根据键的“自然排序”进行迭代。此外，它还实现 SortedMap 接口，该接口包含依赖于此排序顺序的方法。默认是按键值的升序排序。6. TreeMap是基于红黑树实现的，HashMap 是一个基于密钥散列的映射，而LinkedHashMap还要加上双向链表。  最后，ArrayMap、SparseArray是Android特有的集合，后面有时间再写。4 参考引用1. 字节跳动Android面试指南2. Java学习：List接口3. 从源码角度认识ArrayList，LinkedList与HashMap4. JAVA容器-自问自答学HashMap5. 什么是HashMap？6. Java 8系列之重新认识HashMap- 美团技术团队7. Java基础之ConcurrentHashMap8. ConcurrentHashMap底层实现原理(JDK1.7 & 1.8)9. hashmap的21条问题10. LinkedHashMap 源码详细分析（JDK1.8）11. 【JDK1.8】JDK1.8集合源码阅读——LinkedHashMap12. TreeMap源码分析13. 集合之TreeMap（含JDK1.8源码分析）14. 【JDK1.8】JDK1.8集合源码阅读——TreeMap（一）15. 【JDK1.8】JDK1.8集合源码阅读——TreeMap（二）5 下载参考1：提取码： 管理员设置 回复 可见隐藏内容

1.原因网上找了很多的，还有一些在线的，求出来的值五花八门，后来以高德求出来的数据为准。高德两点长度链接：高德经纬度两点长度2.方法2.1.维基百科推荐使用Haversine公式（没有测过，不知道准不准）参考：https://www.cnblogs.com/zhoug2020/p/8993750.html稳妥起见，这里还是采用Haversine公式。 其中 以下是实现代码：using System; using System.Collections.Generic; using System.Linq; using System.Text; namespace HarvenSin { class Program { /// <summary> /// 根据经纬度，计算2个点之间的距离。 /// </summary> /// <param name="args"></param> static void Main(string[] args) { //39.94607,116.32793 31.24063,121.42575 Console.WriteLine(Distance(39.94607, 116.32793, 31.24063, 121.42575)); } public static double HaverSin(double theta) { var v = Math.Sin(theta / 2); return v * v; } static double EARTH_RADIUS = 6371.0;//km 地球半径 平均值，千米 /// <summary> /// 给定的经度1，纬度1；经度2，纬度2. 计算2个经纬度之间的距离。 /// </summary> /// <param name="lat1">经度1</param> /// <param name="lon1">纬度1</param> /// <param name="lat2">经度2</param> /// <param name="lon2">纬度2</param> /// <returns>距离（公里、千米）</returns> public static double Distance(double lat1,double lon1, double lat2,double lon2) { //用haversine公式计算球面两点间的距离。 //经纬度转换成弧度 lat1 = ConvertDegreesToRadians(lat1); lon1 = ConvertDegreesToRadians(lon1); lat2 = ConvertDegreesToRadians(lat2); lon2 = ConvertDegreesToRadians(lon2); //差值 var vLon = Math.Abs(lon1 - lon2); var vLat = Math.Abs(lat1 - lat2); //h is the great circle distance in radians, great circle就是一个球体上的切面，它的圆心即是球心的一个周长最大的圆。 var h = HaverSin(vLat) + Math.Cos(lat1) * Math.Cos(lat2) * HaverSin(vLon); var distance = 2 * EARTH_RADIUS * Math.Asin(Math.Sqrt(h)); return distance; } /// <summary> /// 将角度换算为弧度。 /// </summary> /// <param name="degrees">角度</param> /// <returns>弧度</returns> public static double ConvertDegreesToRadians(double degrees) { return degrees * Math.PI / 180; } public static double ConvertRadiansToDegrees(double radian) { return radian * 180.0 / Math.PI; } } }2.2.第二种方法：参考：https://www.cnblogs.com/zhoug2020/p/3950933.html以下是实现代码（Java）：private static final double EARTH_RADIUS = 6378137;//赤道半径(单位m) /** * 转化为弧度(rad) * */ private static double rad(double d) { return d * Math.PI / 180.0; } /** * 基于余弦定理求两经纬度距离 * @param lon1 第一点的精度 * @param lat1 第一点的纬度 * @param lon2 第二点的精度 * @param lat3 第二点的纬度 * @return 返回的距离，单位km * */ public static double LantitudeLongitudeDist(double lon1, double lat1,double lon2, double lat2) { double radLat1 = rad(lat1); double radLat2 = rad(lat2); double radLon1 = rad(lon1); double radLon2 = rad(lon2); if (radLat1 < 0) radLat1 = Math.PI / 2 + Math.abs(radLat1);// south if (radLat1 > 0) radLat1 = Math.PI / 2 - Math.abs(radLat1);// north if (radLon1 < 0) radLon1 = Math.PI * 2 - Math.abs(radLon1);// west if (radLat2 < 0) radLat2 = Math.PI / 2 + Math.abs(radLat2);// south if (radLat2 > 0) radLat2 = Math.PI / 2 - Math.abs(radLat2);// north if (radLon2 < 0) radLon2 = Math.PI * 2 - Math.abs(radLon2);// west double x1 = EARTH_RADIUS * Math.cos(radLon1) * Math.sin(radLat1); double y1 = EARTH_RADIUS * Math.sin(radLon1) * Math.sin(radLat1); double z1 = EARTH_RADIUS * Math.cos(radLat1); double x2 = EARTH_RADIUS * Math.cos(radLon2) * Math.sin(radLat2); double y2 = EARTH_RADIUS * Math.sin(radLon2) * Math.sin(radLat2); double z2 = EARTH_RADIUS * Math.cos(radLat2); double d = Math.sqrt((x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2)+ (z1 - z2) * (z1 - z2)); //余弦定理求夹角 double theta = Math.acos((EARTH_RADIUS * EARTH_RADIUS + EARTH_RADIUS * EARTH_RADIUS - d * d) / (2 * EARTH_RADIUS * EARTH_RADIUS)); double dist = theta * EARTH_RADIUS; return dist; }